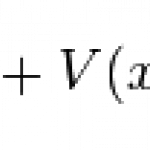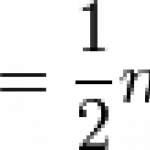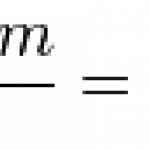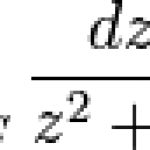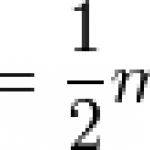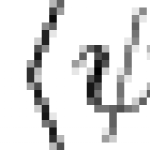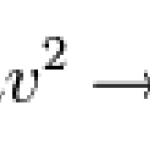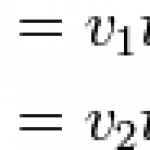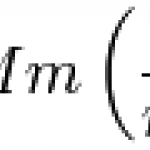Worked Problems

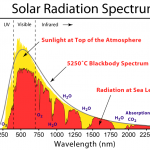
I had an interesting question posed to me recently: how frequently does the sun emit photons with an energy greater than 1 TeV? All of you know about the experiments going on at the LHC, where particles are accelerated to an energy which is equivalent to an electron being accelerated through a potential difference of trillions of volts (which is what a "trillion electron volts" - a TeV is). During the ensuing collisions between particles, high-energy TeV photons are produced. Of course everything is emitting light in the form of blackbody radiation all the time. Human beings emit mostly long-…

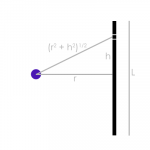
A reader emailed me a fun question from a physics exam he took, along these lines: A car driver going at some speed v suddenly finds a wide wall at a distance r. Should he apply brakes or turn the car in a circle of radius r to avoid hitting the wall? My first thought was that surely the question wasn't doable without more information, but it turns out that we do have enough to give a straightforward answer. Let's take the "turns in a circle" and "slams on brakes" scenarios one at a time. Turns in a circle: Velocity is a vector whose magnitude is the speed and whose direction is the direction…

So consider the one-dimensional time-independent Schrodinger equation: In some ways it's not really an equation as such, because you have to plug in some function V(x) that describes the potential in the problem you're solving. When you first learn quantum mechanics you'll learn the big ones: V(x) = 0, V(x) = V > E, V(x) = 1/2 kx^2, V(x) = k/x, etc. One that's conspicuously absent is usually one of the simplest looking potentials: V(x) = -Fx. That's just the potential of a constant force, say a particle in a uniform gravitational field. Rarely do textbook authors bother to work out a…

The new academic year is starting, and if there's one thing students love it's a good word problem. If Sue is four times as old as John will be when Sue is one year than John... So in that spirit I was amused to find basically this kind of problem in a college physics textbook I was perusing for post ideas as I get back into the swing of blogging. It runs thusly: A father racing his son has half the kinetic energy of the son, who has half the mass of the father. The father speeds up by 1.0 m/s and then has the same kinetic energy as the son. What are the original speeds of the father and the…

There's a classic problem in physics textbooks which asks you about astrology. It's sometimes said - the problem will tell you - that the gravitational pull of the doctor delivering you is stronger than that of Jupiter, therefore it's unlikely that the planets are exerting a whole lot of influence on your life. The problem asks you to check this. Of course gravity is not generally purported to be the conduit of the supposed influence of the zodiac, but it's an interesting problem. And in fact it will turn out that Jupiter generally has the doctor beat, but not by that much. It's a neat…

If you happen to be in the Bryan/College Station area tomorrow, you might consider checking out the Texas A&M Physics Festival. It's sort of an open house with a ridiculous number of top-notch physics demonstrations as well as some very interesting talks. It's free! I'll be there helping out with some of the optics demos. While we're here, we may as well do some physics. This problem is from Halliday, Resnick, and Walker 14.62. It asks (fitting well with the space stealth theme from earlier): One way to attack a satellite in Earth orbit is to launch a swarm of pellets in the same…

First of all, happy Thanksgiving everyone! I hope you spend the day happily with the people you care about, and remember to spend a moment or two reflecting on the things for which you're thankful this year. Now on with the show: Back when I first started writing this blog, I focused mostly on problem solving. The goal was to bridge the gap between popularization and textbook. I was always doubtful there was much of a market for this, but of course there are at least some interested people and especially since writing is so fun I was and am I'm more than happy to fill that gap. Over the…

I shot an arrow into the air, It fell to earth, I knew not where; For, so swiftly it flew, the sight Could not follow it in its flight. - Henry Wadsworth Longfellow This is what happens when you don't pay attention in freshman physics. You don't need to see where the arrow goes to find out where it lands, you just need the initial speed and angle. Two simple accelerated motion equations later, you have the range. The method isn't perfect since it fails to account for air resistance and other factors, but for finding an arrow it's a lot better than shrugging and giving up once you lose…

Note to the reader: this post is relatively stiff mathematically. For those not mathematically inclined, I think you might enjoy reading it anyway and enjoying it as you would a tour of a widget factory; even if you're not worried about the details of the nuts and bolts, it's fun to see it done. While watching football yesterday, I got a phone call from a great friend whom I first met in our halcyon high school days. He's a fellow physics student a few years younger than me, calling to discuss a problem in contour integration. Most people like watching football more than they like doing…

This guy is Allo Diavolo: He was a circus daredevil. At the dawn of the 20th century he worked on a number of stunts dressed in his ominous horned outfit. These days a lot of people, including me, have heard of him as an example in the pages of physics textbooks. In my case it was Halliday and Resnick, a standard (and good) freshman physics text. Diavolo did a trick where he looped the loop riding a bicycle. It's pretty impressive: The breathless circus ad copy claims that this stunt is more or less certain death. It wasn't, of course. I wouldn't want to try it, but it's certainly a…

This week the science blogosphere has been spending a lot of time on space exploration and the science of understanding the universe outside our own planet. At risk of being the buzzkill distracting from all the cool space travel history and heated debates about NASA's future, I think it will be interesting to do a little bit of the math behind basic rocketry. As a bonus, we'll do it in the Lagrangian formulation of classical mechanics. (And maybe to draw in a few Google hits from lost students, I'll note that this is pretty much Goldstein 1.13) Non-mathy readers don't have to worry about…

We haven't done an actual straight-up physics problem in a while, much less one above the level of undergraduate freshman physics. There's a reason: it's roughly as niche as it's possible for an internet post to be. But on the other hand, surely someone ought to do it every once in a while. So here we go with a roughly 3rd-year undergrad physics major problem in quantum mechanics. If you've not studied it before, fear not! As always I'll try to convey the overall path without relying on the details of the math. Consider a particle in a one-dimensional square well (0 2 for some small α.…

Spider-Man, of mass 90kg, is perching 10 meters above the ground when he notices his (depending on the continuity) crush/girlfriend/wife Mary Jane (50 kg) being menaced by... I dunno, a menace. I'm more of a DC fan really. He swings down toward her to spirit her our of harm's way. Assuming he starts from rest and lets gravity do the work, how fast is he going just before he reaches her? Well, he has a gravitational potential energy mgh. And just before he reaches her, it's all been turned into kinetic energy, half the mass times velocity squared. Fig. 1: A free-body diagram. Which works…

Every section of Physics 218 I've taught this semester has asked me about this question. Really it's less of a physics question than it is a math question, but either way it gives people fits. It's not all that surprising. While it seems like it should be simple, to most beginning students it's not at all intuitive how all the given information gits together. Without further ado, the problem: Earthquakes produce several types of shock waves. The most well-known are the P-waves and the S-waves. In the earth's crust, the P-waves travel around 8.9 km/s while the S-waves move at about 2.7 km/…

Poking around on the internet looking for interesting problems to assign the students I'm about to have this semester, I came across this one: How much energy must a 450 kg cow expend in jumping over the moon? Fig. 1: Buzz Cowdrin? Now hints and solutions are available on the linked site, so what I'd like to do is just talk conceptually for a moment. Leaving aside for the moment the derivation of the equation, it will turn out that the energy required for a cow (or anything else) to reach a particular elevation is given by a particular potential energy equation: G is the universal…