“If everything was perfect, you would never learn and you would never grow.” -Beyoncé
As human beings, we may be far from perfect. Even our mathematical celebrations, like Pi Day, are mere approximations. But there are a few mathematical quantities out there that really are perfect. And today, June 28th, I'd like to share with you a celebration we should all be able to partake in: perfect number day!
Image generated by me.
Most numbers are deficient, in the sense that if you added up all their divisors (other than themselves), you get a number less than the original one you began with. A few of them -- about 24.8% of the countable numbers -- wind up being abundant, or with a number greater than the original one you began with.
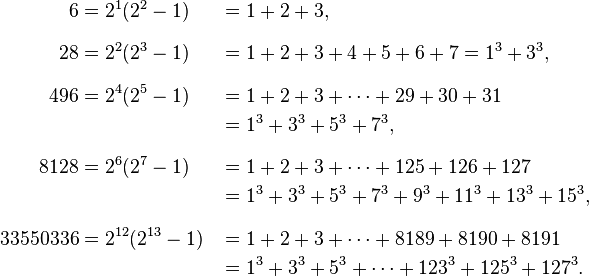Image credit: screenshot from the Wikipedia page on Perfect Numbers, via http://en.wikipedia.org/wiki/Perfect_number.
But a select few of them -- with only 48 known so far -- are perfect. Go read the whole story of them here!
- Log in to post comments
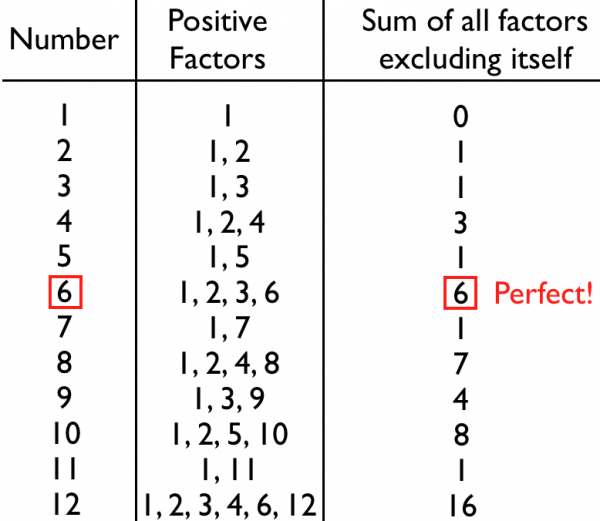
"It has been proven that all the even perfect numbers that exist are of the form (2^n - 1)"
I think there must be a typo, or other mistake in this sentence, as (2^n-1) seems definitely odd to me. Unless there's a definition of "even perfect number" that I somehow overlooked.
Sorry, that should have read "It has been proven that all the even perfect numbers that exist are of the form that are generated by Mersenne primes that follow (2^n - 1)," and that has been fixed.
Thanks for the catch!