"The layman always means, when he says "reality" that he is speaking of something self-evidently known; whereas to me it seems the most important and exceedingly difficult task of our time is to work on the construction of a new idea of reality." -Wolfgang Pauli
On the surface, it shouldn’t appear to make all that much difference to the Universe whether a particle has a spin in half-integer intervals (±1/2, ±3/2, ±5/2) or in integer intervals (0, ±1, ±2). The former is what defines fermions, while the latter defines bosons. This hardly seems like an important distinction, since intrinsic angular momentum is such a nebulous property to our intuitions, unlike, say, mass or electric charge.
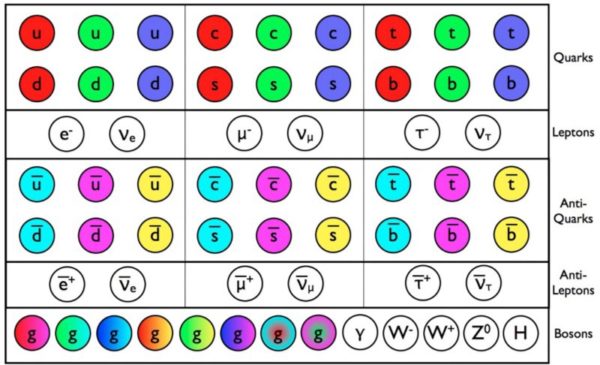The known particles in the Standard Model. These are all the fundamental particles that have been directly discovered; the graviton, although undiscovered, would be a spin=2 boson. Image credit: E. Siegel.
Yet this simple, minor difference carries with it two incredible consequences: one for the existence of distinct particles for antimatter and one for the Pauli exclusion principle, that are required for matter as we know it to be. Without these differences, and without these rules, it’s simply a matter of fact that the atoms, molecules and living things we see today wouldn’t be possible to create.
The way that atoms link up to form molecules, including organic molecules and biological processes, is only possible because of the Pauli exclusion rule that governs electrons. Image credit: Jenny Mottar.
- Log in to post comments
More like this
What a huge difference a half-integer spin makes!
Colliding a photon with another photon though, under the right conditions, will cause a form of pair production, and it will become an electron-positron pair. What happens when two Z bosons of the weak interaction come together like that? Or gluons? Just a glueball?
@Anonymous #2: Z0 annihilation has not been directly observed (because we can't make Z0 beams, of course), but the production of Z0 pairs in high energy collisions (at LEP2 and the Tevatron) has been observed. The principle of "detailed balance" means that you can invert that interaction to recognize that a Z-Z collision can produce the accelerator original state. The result should be equivalent to gamma-gamma (or more precisely gamma*-gamma*) interactions, with some pair of particles produced.
Another outstandingly good non-short post from Ethan. He's terrific at the short pieces too. What an expositor in print. I suppose I must buy his book now.