heat
cmonforton | May 9, 2017The southern U.S.’s construction boom is not translating into better wages and working conditions for construction workers. Those are the results of a survey of 1,435 construction workers from six southern U.S. cities: Atlanta, Charlotte, Dallas, Houston, Miami, and Nashville. The survey, which was administered during July and August 2016, was a collaboration between the Texas-based Workers Defense Project, the Partnership for Working Families, and Nik Theodore, PhD with the University of Chicago's Department of Urban Planning and Policy. Their report, Build a Better South, was released…
dr. dolittle | December 9, 2016 Image by Botaurus - Wikimedia commons
A changing climate has the potential to greatly impact ectotherms, which depend on the environment to regulate their own body temperatures. In a new study published in the American Journal of Physiology- Regulatory, Integrative and Comparative Physiology, researchers were curious how exposure to varying temperatures would affect developing ectotherms. They answered this question using Drosophila melanogaster, commonly known as fruit flies. They exposed freshly laid eggs to ten different temperatures ranging from 12 to 32°C, the upper and lower limit of…
cmonforton | September 21, 2016The temperature yesterday in Austin, TX was 97 and the heat index was 104. My USPS mail carrier was feeling the heat in more ways than one.
As is the case most mornings, we exchange waves with each other. He begins his rounds in my neighborhood around 8 am and I’m using walking 12 year-old Laredo, our golden retriever. Laredo and I walked passed his mail truck. I noticed a white sedan stopped behind it. When the mail truck proceeded to the next mail box, the sedan followed slowing behind it. The person driving the sedan was wearing a neon safety vest. I wondered, “management monitoring his…
gregladen | December 28, 2015I had considered writing an accounting of all the outlandish weather events of 2015, but that project quickly became a tl:dr list of untoward happenings which is both alarming and a bit boring, since it is so long. So, I decided to generate something less comprehensive, focusing more on the context and meaning of the diverse and impressive set of outcomes of anthropogenic global warming, an historically strong El Niño, and, well, weather which is already a pretty whacky thing.
See: Highlights of Climate Change Research in 2015
It should be noted right away that 2015 is the last year in which…
dr. dolittle | June 19, 2014
Shivering is one mechanism by which heat is produced in the body. Heat production is called thermogenesis. Another mechanism is through nonshivering thermogenesis regulated by brown fat (i.e. adipose). This second type of heating mechanism kicks in when we need extra heat production such as a postnatal infant, someone developing a fever, an animal arousing from hibernation, eating, or in the case of the current study, stress.
A recent study published in the American Journal of Physiology provides evidence that during stressful events brown adipose tissue can elevate body temperature through…
pgleick | May 20, 2014I previously posted a summary of the water-related conclusions from the new National Climate Assessment, recently released after three years of writing, review, and analysis. The following “findings” are a broader summary of the results from the newly released National Climate Assessment (NCA). They are by no means a full summary: far more detail can be found in the chapters and the regional syntheses, but these are noteworthy conclusions. (Note, thanks to Tim Smith – Sustainable Water Resources Coordinator – for highlighting these. The page numbers refer to the NCA Summary)
1. Global climate…
lborkowski | July 22, 2013Many of us have been complaining about the heat that’s blanketed much of the country for the past couple of weeks, but the situation is especially severe for those who work outdoors or in spaces without adequate cooling.
The Occupational Safety and Health Administration is investigating the death of James Baldassarre, a 45-year-old postal worker who collapsed on the job and died in Massachusetts last week. Baldassare had worked for the US Postal Service for 24 years; his wife, Cathy, told WCVB News, “"I have a bunch of texts from Jimmy all day long, saying, 'I'm going to die out here today.…
dr. dolittle | October 11, 2012
Hair on an Asian elephant (right) compared to an African elephant's head (left). Image taken by: Conor Myhrvold
Researchers think that the hair on an elephant might actually function to keep the animals cool as opposed to keeping them warm as it does for other mammals. Living in hot climates (as high as 122 degrees F) since the last ice age means the animals have had to evolve ways to tolerate the heat. Until now, it was only known that elephants kept cool by dissipating heat from their ears (circulating warm blood to their large flat ears, where the heat could escape, and returning the…
lborkowski | April 30, 2012by Kim Krisberg
It was a lucky winter for Becky Belmont. The weather was on her side.
As the director of energy and weatherization at West Central Minnesota Communities Action Inc., Belmont was sure the agency would run out of energy assistance funds to help all those in need. But fortunately, a mild Minnesota winter translated into fewer residents who needed help keeping their homes warm this year.
Today, Belmont seems pretty optimistic that even with declining funds, the agency will have enough funding to last through May 31, which marks the end of its Energy Assistance Program year. This…
lborkowski | October 4, 2011If you haven't already seen Spencer Scoper's in-depth story on working conditions at Amazon.com's Lehigh Valley warehouse, it's well worth a read. The Morning Call's investigation into the warehouse involved interviews with 20 current and former warehouse workers, and most of them were temporary employees hired by Integrity Staffing Solutions rather than Amazon itself. Workers reported that they were expected to maintain a demanding units-per-minute rate -- and it became especially hard to keep up the pace when summer temperatures inside the warehouse soared above 100 degrees. Scoper writes:…
vlicata | September 23, 2010The laws of thermodynamics are empirical laws - they were not derived from some first principles of the universe: they were derived by doing thousands and thousands of experiments, and then coming up with some relationships that could quantitatively explain all those experiments.
In biological thermodynamics, we are at the beginnings of trying to define a similar set of "laws of biothermodynamics" - in this case we want relationships that connect thermodynamic quantities (ÎG, ÎH, ÎS, ÎCp) to functional or structural information about the biomolecules themselves. Nobody has anything that…
vlicata | September 16, 2010Scienceblogs is promoting the writing of "Science 101" general topic posts all through the "back to school" month of September. So, here is the first in a multi-part series on Heat Capacity in Biology:
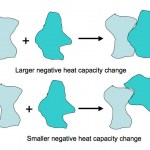
Heat Capacity in Biology 101: What is it?
Heat capacity is basically a proportionality constant. For any substance, the heat capacity tells you how much the temperature of the substance will change when you add a specific amount of heat.
Here is an absolutely beautiful schematic illustration of the difference between a small heat capacity and a large heat capacity (from a website on the…
rallain | June 7, 2010As part of the Ask a ScienceBlogger series, reader Jim Swanson asks:
When I open the dishwasher after washing and the contents are still hot, why do the glass and ceramic items dry off more quickly than the plastic items?
This is a great question. Great because it is something most everyone can relate to and great because there is some good science. Really, this shows the difference between temperature and thermal energy. I think the common idea is that temperature is a measure of the energy something has - but this isn't quite true.
Ok, let me first start with a sample case. Suppose you…
edyong | March 14, 2010Take a whiff of mustard or wasabi and you'll be hit with a familiar burning sensation. That's the result of chemicals in these pungent foods hitting a protein called TRPA1, a molecular alarm that warns us about irritating substances. The same protein does a similar job in other animals, but rattlesnakes and vipers have put their version of TRPA1 to a more impressive and murderous purpose. They use it to sense the body heat of their prey.
Pit vipers are famed for their ability to detect the infrared radiation given off by warm-blooded prey, and none more so than the western diamondback…
sastyk | February 11, 2010
You'd be surprised at how warm our barn is on winter nights. A few nights ago, the thermometer read -10 as I headed out the door, and the wind was howling, but inside the barn it was below freezing, but surprisingly tolerable. Close down a comparatively small space, insulate the floors with dry bedding and fill it with warm life, and the combined body heats make it surprisingly pleasant.
Up in the rafters, some of the chickens and the turkeys are nested for the night, and they snuggle together. In the rest of the barn, they also nest in a heap. The goats snuggle together for warmth,…
rallain | July 18, 2009Note to self: don't do the mechanical equivalent of heat lab again. It doesn't really work that well and there are better labs to do.
So, what is the mechanical equivalent of heat lab? It is actually a pretty cool idea. Take and object and drop it. What happens to the kinetic energy the object had right before it hit the ground? Most of it goes into thermal energy of the object and surroundings. In this lab, the students measure the change in gravitational potential energy for a falling object (where object is really lead shot or something) and then measure the change in temperature in…
rallain | March 24, 2009There are some really cool questions out there. Questions that do not require a lot to ask and do not require a lot to answer. Here is one such question (I can't remember where I first found this question or something like it):
Suppose you put take two identical cans of soda out of the fridge and place them on the floor in the middle of a room. One can you leave alone and one can you cover with a wool blanket. After an hour, you come back and check on the two cans of soda. Which will be warmer?
First, why do I like this question? Mainly because everyone can give an answer. If asked…
rallain | August 26, 2008Heat. You have heard it before. You have used it. I have even used it. Do we need this word? No. Is this a useful word? No.
Let me start with the definition as usually stated in a physics type text: (this is from [dictionary.com](http://dictionary.reference.com/browse/heat))
*heat:* a nonmechanical energy transfer with reference to a temperature difference between a system and its surroundings or between two parts of the same system.
This definition is fine. It is not wrong, but is it needed? Not really. Couldn't we just say energy transfer? Actually, I like to use this in the…