The Physics of the Ponytail

The first major computer-animated film was Toy Story. It had a few human characters, most prominently Andy (who spends most of the film wearing a hat) and Sid (who sports a buzz cut). The focus of the film is on the plastic toys.

One of the major reasons for this is the fact that toys are pretty simple. They have just a few moving parts for the computer to keep track of during the rendering process. People have many more. Every hair on a person's head really consists of many moving parts, since it can bend anywhere along its length to various degrees. And there are around a hundred thousand hairs which interact with each other, applying force to the other hairs they touch. Since it's pretty much impossible to place every computer-animated hair by hand, if you want convincing hair in your animated films you need a good model for how the physics of hair works.

By the time Toy Story 3 came around, faster computers and better knowledge of how hair behaves made the problem of animating humans a lot more tractable:

Now we're one step farther in our understanding of hair, with an interesting research article in Physical Review Letters:

Phys. Rev. Lett. 108, 078101 (2012)
Raymond E. Goldstein, Patrick B. Warren, and Robin C. Ball
Shape of a Ponytail and the Statistical Physics of Hair Fiber Bundles

They've attempted to create a model of why ponytails have the shape they do. They postulate that the energy of a bundle of hair is a function of the average curvature of the hairs (ie, the overall shape of the ponytail), the potential energy due to the gravitational field of the earth, and and average force per length due to the statistical properties of the individual hairs - their points of contact, waviness, split ends, whatever. The equation from the paper is:

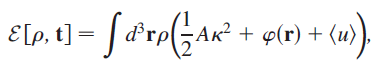Where the κ term is the average curvature, the φ term is the gravitational potential, and the u term is an average over the statistics of the individual hairs. How well does it work? Pretty well:

Pretty good, especially for a model which is effectively two-dimensional.

You might wonder why anyone would bother researching this. (This particular work even won an Ig Nobel prize.) Like many seemingly weird bits of science, there's actually quite a bit of practical point to it. Many-body problems are hard, and any advance that allows you to avoid having to do a full-blown simulation has the potential to be extremely useful. I mentioned computer animation as a flashy example, but this research is useful in any kind of bundled-fiber system from fiber-optics telecommunications to the medical treatment of the fiber bundles in your body.

For a five-second hairstyle, that's not a bad day's work.