“The joy of life consists in the exercise of one’s energies, continual growth, constant change, the enjoyment of every new experience. To stop means simply to die. The eternal mistake of mankind is to set up an attainable ideal.” -Aleister Crowley
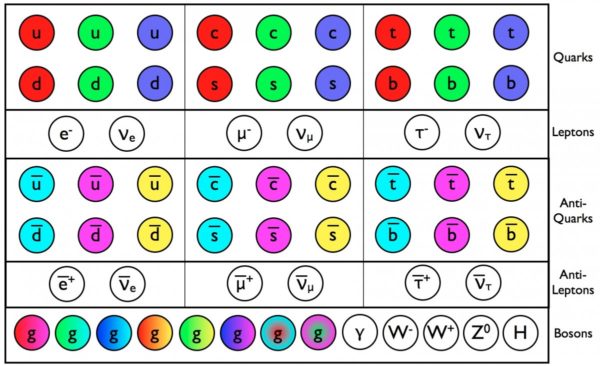
As we learn more and more about the Universe, we'd like to describe it as simply as possible. While we have thousands or even millions of chemical configurations, they arise from less than 100 different atoms. Atoms themselves are made up of protons, neutrons and electrons. The great hope of unification and for fans of elegance in general is that all of the Universe can be derived from as simple a formulation as possible.
But with the zoo of particles we have today, the gravitational, strong, weak and electromagnetic forces plus the way everything interacts, it takes a larger number of fundamental constants than we might like to reproduce our Universe. And even at that, they don't give everything! Without a surefire path to the matter/antimatter asymmetry, dark matter, or a lack of strong CP-violation, among others, there are likely even more constants than the ones we know we need.


Aleister Crowley? Really?
If 'initial conditions' are very close it will not produce an exact outcome of our Universe but a similar 4 dimensional Standard Model Universe with near similar dimensionless constants. To obtain the very exact same 'initial conditions' which would produce an exact replica of our Universe might be very improbable. This might produce a vast array of similar Universes as the 'initial condition' spectrum may be very large.
Lloyd, got a problem with the content of the quote? Then come out with it.
Hitler probably said "I love you, mummy" but are you going to insist that loving mum is wring because Hitler said it?
Really?
The onset of our epoch in the evolution of the universes infinite evolution that is the expression of its energetic force. Everything that we see is only the result of energetic expression that existed after recombination about 180,000 yr after the Big Bang. Electromagnetic energy itself,at 71/2 x around our planet in a second is dark energy to us within our plane of reference. We only see its reflected images after it has been stopped and transmuted to other wavelengths in objects that we can then recognize.Pure electromagnetic energy is dark energy to us. We only perceive it's effect after the fact.(neutrinos are also energetic expressions similar to electromagnetic waves themselves. Unlike EMwaves they still pass right through what we think are solid objects without slowing down).
So, a quark, a boson, and a fermion walk into a bar.
Josh, with all due respect (none) that was a load of tosh. Eliza managed better than that.
Text, in the absence of context, amounts to pretext.
AC has pretty well defined his particular context which historically included many items quite unsuitable to polite society or even one's sanity for that manner. If such quote is attributable to AC, his context was likely having to deal with whether a male child might better serve as sacrifice to summon some ancient demon form better than a female one... this time.
Lloyd, that too was content free blubbering.