The Pythagorean theorem made a big impression on me when I first saw it in middle school. It was probably the first genuinely non-trivial theorem that I learned. The theorem is simple to state and to understand, but it is not at all obvious. I have a clear memory of my sixth grade math teacher, Ms. Oswald, showing it to me, and having my reaction be, “No way!”
The theorem, of course, states that if a right triangle has sides a,b,c, with c representing the hypotenuse, then we have the equation
$latex a^2+b^2=c^2$
More geometrically, we can say that the square on the hypotenuse is equal to the sum of the squares on the other two sides. There are literally hundreds of proofs out there, many of them quite beautiful. Recently, though, I came across one I had never seen before. It strikes me as especially clever and elegant, so I thought I'd show it to you. Here we go:
Given your right triangle, construct a circle whose radius is c and whose center is one of the non-right angle vertices of the triangle. The result will look something like this:
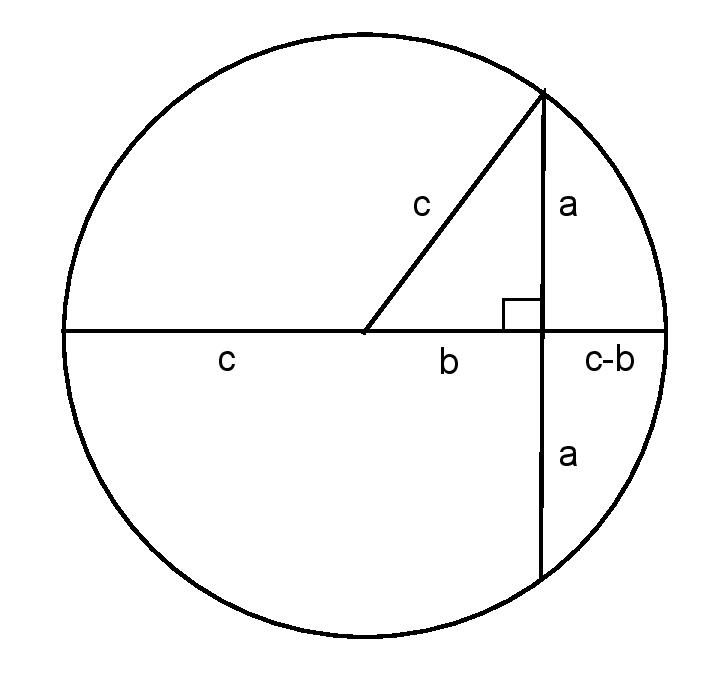
You will notice that I went ahead and labeled some of the lengths. I think the labels along the diameter are clear enough, as are the labels along the sides of our original right triangle.
I have taken the liberty of extending the side of length a. Now, I will need you to recall the theorem that states that in a circle, a diameter that is perpendicular to a chord bisects that chord. That is why the two parts of the chord are both labeled with an a.
I will now need you to recall another basic circle theorem. When two chords in a circle intersect, each chord is divided into two pieces. Suppose one of the chords is divided into pieces of length x and y, while the other is divided into pieces of length f and g Then it must be the case that xy = fg.
Let us apply this theorem to our present circumstance. We have one chord divided into two pieces, each of length a. The other chord is the diameter, and it is divided into pieces of length (c+b) and (c-b). Thus, it must be true that
$latex a^2=(c+b)(c-b)=c^2-b^2$,
and that's the Pythagorean theorem!
I think that's pretty nice. How about you?

The one that seems most intuitively-satisfying to me is the square whose sides have length a+b, with a square of side length c formed inside it by using the four corners of the outer square as the right-angles of a-b-c right triangles. I wish I could draw it in this comment. Anyway, by equating the area of the outer square to the area of the inner square plus the four right triangles, one gets (a+b)^2 = c^2 +2ab.
That's really cute.
Of course, we have to check that the proof of the circle theorem does not depend upon Pythagoras itself.
JimV, that's my favourite proof as well! Here's a the picture you wanted to draw: http://i.stack.imgur.com/Wjxmq.png
I like this proof but it's not as elegant as it looks because it hides most of the argument inside the intersecting chords theorem. I think it'd be better to include the proof of that as well (it's not hard) rather than asking the reader to take it as a magic black box.
Steven Carr--
It doesn't! The theorem about the two chords is proved using similar triangles and makes no use of the Pythagorean theorem at all.
"Now, I will need you to recall the theorem that states that in a circle, a diameter that is perpendicular to a chord bisects that chord."
I don't recall it but let me see if I can prove it. I draw the radius from the center to the lower point where the chord meets the circle. I now have two triangles with one side equal to c, one side equal to b and a common right angle. Now, ordinarily side-side-angle is not enough to allow us to conclude that congruence holds but I found the following proof http://mathforum.org/library/drmath/view/54659.html that allows us to conclude that it holds in this case, since c>b, without using the Pythagorean theorem.
Jr--
Yes, your proof is correct. And good observation that the “hypotenuse-leg” theorem can be proved without using the Pythagorean theorem. That is, in right triangles, SSA works!
I like this one and so do my pupils.
https://www.youtube.com/watch?v=CAkMUdeB06o
I hadn't seen that before. Very cool!
I've always like the simple illustration Jacob Bronowski did in the Ascent of Man. You can see it without any math knowledge, etc. If you have the book (paperback, 1973) it is on page 159.
I'll try to describe: He made 4 copies of a right triangle out of wood, and created a square with them that had sides of length 'c'. The triangles covered all but a central square (having sides of length 'a' minus 'b'). He then created a square of that size. So the total area of the 4 identical triangles plus the central square is 'c' squared. He then rearranged the 4 triangles thusly: take two triangles and create a rectangle of size 'a' x 'b', and do the same with the other two. Place the two rectangles against each other, one oriented 90 to the other, forming an 'L' shape. Place the central square piece in the "crotch" of the 'L', place a straight line (he used a stick) along the outer edge of the central square piece, dividing the object into two squares. From inspection it is clear that one square is 'a' squared, and the other is 'b' squared. Ergo, a^2 + b^2 = c^2
I'll see if I can send you a photo of that page.