"Nothing in the universe can travel at the speed of light, they say, forgetful of the shadow's speed." -Howard Nemerov
I know many of you are still mad at the night sky because of the full Moon preventing you from seeing the recent, close-by supernova in the Pinwheel Galaxy, at least until the end of the week.
With the full Moon brightly illuminating your sky (and filling it with light pollution), only the brightest, most compact objects are visible at most locations on Earth.
But there is one object -- rising at about 9:30 PM each night, these days -- that's not only visible to the naked eye, but one of the night sky's grandest sights through any telescope, large or small.
The planet Jupiter! In fact, those of you with the extraordinary patience to track our Solar System's largest planet over the course of a few hours will not only have the chance to see Jupiter and its four Galilean moons, you'll get to see them in action!
In particular, the innermost of Jupiter's Moons, Io, completes one revolution around Jupiter in an incredibly precise 42 hours, 27 minutes, and 33.5047 seconds. (Yes, we really do know it to that accuracy!) Every time Io passes in front of Jupiter -- and it does this about four times every week -- it casts a shadow onto Jupiter's surface, creating a solar eclipse.
But what's more interesting for our purposes is that every time Io heads behind Jupiter, the gas giant's mightly shadow plunges its satellites into darkness, causing a lunar eclipse.
This can result, depending on where Earth in is its orbit relative to Jupiter and the Sun, in one of Jupiter's moon's seeming to eerily "appear" out of nowhere, some distance away from the edge of Jupiter itself.

Animation credit: Robert J. Modic, over a mere 10-minute timespan! Image was processed down from 3.2 MB to a mere 274 kb by Cleon Teunissen.
This is just geometry at work here, of course. By time the 1670s came around, it was universally recognized (among astronomers, at any rate) that the planets of our Solar System all orbited the Sun, with the Earth being an inner (and hence faster) planet as compared to Jupiter.
During six months out of the year, the Earth would be approaching Jupiter (at point B), for example, at the points F and G. When this happens, whenever one of Jupiter's moons reaches point C, above, it disappears into Jupiter's shadow.
During the other six months, the Earth recedes away from Jupiter, for example, at points L and K. During this time, whenever one of Jupiter's moons reaches point D, it appears to emerge from Jupiter's shadow.
However -- and here's the interesting part -- it appears to take longer for a moon, like Io, to emerge from Jupiter's shadow when you're at point K as compared to point L! And by the same token, it appears to take longer for a moon to plunge into Jupiter's shadow when you're at point F as compared to point G! What gives?

In the early 1600s, it was known that the speed of light was very, very fast, but it wasn't known whether it was infinitely fast or not. The only experiment done to measure it was Galileo's experiment in 1638, which I call the Beacon of Gondor experiment.
One night, Galileo sent his assistant out far across the fields, and ordered him to stand at the crest of a hill. Galileo would be atop a distant hill. Galileo would unveil his lantern, so that his light would shine brightly atop the hill, and as soon as the assistant saw the light, he would then unveil his lantern. Galileo reasoned that he would be able to measure the distance between his assistant and himself, as well as the time it took for the light to travel round-trip, and hence he'd be able to figure out the speed of light.
Well, considering that the speed of light is around 300,000 kilometers per second, you can imagine what the results of this experiment, conducted from two hills across a field, were.

Very, very fast, was Galileo's conclusion. But was it infinitely fast, or was it simply too fast to measure between two humans on Earth?
For a couple of generations, the question was unsettled. But in the 1670s, Danish astronomer Ole Rømer not only settled it, he became the first person to measure what the speed of light actually was. All you need to know is where the Earth, Jupiter, and the Sun are positioned, which we knew in great detail thanks to the work of Kepler and Brahe nearly a century prior. Here's what you do.
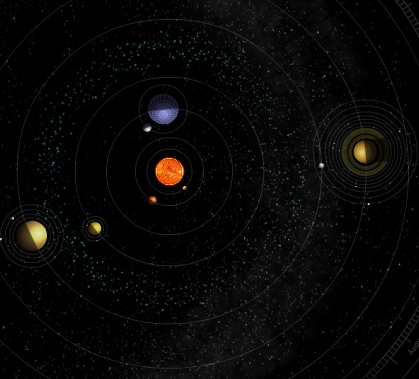
Above is where the Earth, Jupiter, and the Sun were positioned back in June of this year; this corresponds to point "F" in Rømer's diagram from his sketchbook. What you can do is measure when Io appears to complete its transit of Jupiter (when it finishes passing in front of it), and accurately time how long it takes before it plunges into Jupiter's shadow.
Then, wait a few months, until the Earth is at a closer position to Jupiter, but still makes the same angle it did all those months ago when you made your earlier observation. Today, for example, could correspond to point "G" in Rømer's diagram.
Do the exact same thing; time how long from the end of Io's transit until it plunges into Jupiter's shadow. If you've done your measurements accurately and correctly, you will find -- this time -- that it was several minutes shorter than it was a few months ago!
Why would this happen? Let's go back to Rømer's sketch.
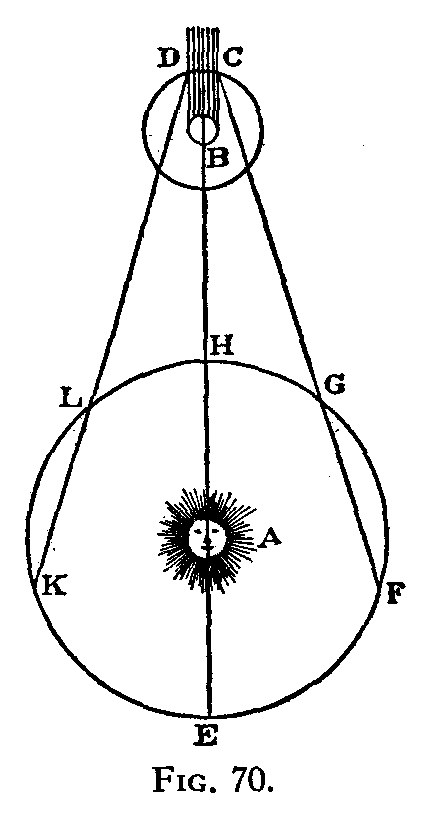
The light emitted by Io, at point C, is the last bit of light we'll be able to see from it before the lunar eclipse begins. If that light traveled infinitely fast, then someone at point G would get the light at the same time as someone at point F, and there would be no difference.
But if the speed of light were finite, that last bit of emitted light would arrive at point G earlier than at point F! If you can determine the distance between point F and point G, and you can measure the time difference between when the moon plunges into shadow (at point C), you can measure the speed of light!
(Of course, you can do it just as easily with the moon re-emerging from Jupiter's shadow -- at point D -- during the other six months of the year.)
In the centuries since, of course, we've refined our measurements of the speed of light, and we've even measured the speed of gravity, which turns out to be the same. It turns out that the original, 1676 measurement was low by about 25%, mostly due to errors in the Earth-Sun distance.
You can do this yourself, with any of Jupiter's four Galilean satellites, with simply a telescope and a clock, and some careful observations over the course of a year. If you'd like to get started, tomorrow night, September 13th, at about 11:24 PM Pacific Daylight Time (sorry folks, it's my time zone), you can see Jupiter's moon Europa plunge into shadow off of its eastern limb.
And that's how we found that the speed of light is not only finite, but were able to measure what it actually was! Not bad for 300 years ago!






"Light pollution" seems to me to be an inappropriate and pejorative term for the magical radiance emitted by our beautiful, mysterious, unique moon, placing it in the same category as that emitted by vulgar street lamps and billboards.
I have always enjoyed the story of how Galileo attempted to measure the speed of light and enjoyed having it reiterated here.
Hi Ethan,
very good post!
I always knew that Römer measured lightspeed via the moons of Jupiter, but never, how he did that...
Thanks a lot.
It turns out that the original, 1676 measurement was low by about 25%, mostly due to errors in the Earth-Sun distance.
Stay tuned... Captain Cook visiting Tahiti...
Hey-
Love your posts in general. But I think your a bit unclear here. No matter if the earth is in position F or G, isn't the time difference between the completion of the transit and the lunar eclipse going to be the same. (The light at the end of the transit had to travel just as far as the light beginning the eclipse.)
What changes as the earth gets nearer or farther is the apparent timing between between each orbit. So if you watch a transit at F and then count in 42 hour 27 minute chunks, when you get to G you are surprised to find the transits happening earlier than you expected. But the time between transit and eclipse should remain (almost) constant.
Anyway, keep up the good work. Love the blog.
-DHF
Rømer had it all sussed but I never understood what he had against "I" and "J". Actually, although Rømer knew how long it took light to cross the Earth's orbit and the size of the orbit he never, so far as we know, divided one by the other to get a velocity.
There are some young-earth creationists who try to claim that the speed of light was much faster in the past. To back that up, they use Romer's measurement, which they say gave a result somewhat more than the present value. But you are saying that his measurement gave a result less than the present value. Can anybody explain this discrepancy?
@csrster (5):
Did you ever tried in "Arial" to identify "l" (el) and "I"?
Moreover in the past everything was written by hand, and very often in LATIN. In handwritings "1", "I", "J" and "l" often are not unified and thus they were avoided.
I have to agree with Dhnice, the explaination is somewhat unclear.
The Wikipedia article http://en.wikipedia.org/wiki/R%C3%B8mer%27s_determination_of_the_speed_… is confusing too. It says: "During those 42½ hours, the Earth has moved further away from Jupiter by the distance LK"
One easy way to understand it, is to think of the Doppler-Effect. As the Earth moves towards Jupiter, the orbital period of Io decreases, and increases as it moves away.
This Wolframalpha demonstration includes an illuminative Formula: http://demonstrations.wolfram.com/RomersMeasurementOfTheSpeedOfLight/
Dhnice and CHP,
It is almost constant; the difference is mere seconds. What you really need, if you want to be accurate, is a table of many values of when one of the Jovian moons plunges into (or exits from) Jupiter's shadow. (Such a table, in astronomy, is known as an ephemeris.)
Since you know the period of the satellite very accurately, you can determine when it actually is plunging into/out of the planet's shadow, and compare that with when you observe it entering/exiting the shadow. Over the course of a year, you'll find variations of up to sixteen minutes or so, where that difference corresponds to the light-travel time of the diameter of the Earth-Sun distance.
This is what Rømer actually did, but it is asking a bit much of any amateur astronomer.
Hi Ethan,
As always, I like your explanations and I thank you for letting us know about the Rømer experiment. I hadn't heard about the story before and thought the speed of light was first measured by Michelson & Morley.
I admire Rømer for his achievement, but I have to ask you this: weren't the points F and K on his drawing somewhat closer to Jupiter than the drawing shows? Otherwise, the Sun would still be visible to the observer, as your picture above the caption "Above image made from a screen capture using this orrery application" clearly shows - am I right?
Tihomir
Tihomir,
You have to be on the "night" side of the Earth in all of those cases, which thankfully you get to do every time the Earth rotates at nearly all latitudes.
Very very nice science.
I did not know.
Thanks.
the next to the last sentence of the article makes no sense as it seems to conclude the the speed of light IS infinite.
Lovely post Ethan.
I remember reading a beautiful essay by Isaac Asimov (probably called 'clock in the sky') on this very subject, and he had mentioned the same thing Dhnice did.. IIRC:
that it was the absolute time of lunar eclipses that seemed off. i.e If we notice Io's first lunar eclipse at T, then the Nth one should be approx' T+N*42.xx (or some such thing that astronomers of those days had already worked out). But they werent. Since accurate clocks were also invented maybe a few decades earlier than that, it seems they started wondering if their clocks were not working properly. And then Romer came up with the explanation. Newton thought that it was pretty cool, but another famous astronomer Cassini didnt agree.
I didnt realize that the moons would disappear (in the shadow) like that until now. Your visuals made it so clear.
I think Ole Rømer's diagram would make an awesome tattoo. Maybe I'll place it next to Darwin's Tree of Life, once I get it that is.
@11:
Ethan,
Exactly that is my point: on the drawing, the night side of the Earth on the points F and K never look towards Jupiter, but away from it. In order for the night side of the Earth to look at least a bit in the direction of Jupiter, the Earth would have to reside somewhere between the 9 o'clock position on the circle and 3 o'clock. The drawing shows the points F and K underneath the 9->3 middle line.
@DHnice: the time taken by the moon to disappear from the edge of Jupiter and make contact with the shadow is exactly the same (provided the viewing angles are the same as explained). However, the time of actual contact with the shadow to the time you observe the light to disappear depends on your distance from Jupiter. SO, when you measure the time between the moon leaving the disc of Jupiter to the total disappearance of the moon, that time will vary depending on your distance from Jupiter. If you were right at Jupiter this may appear instantaneous but as you move further from Jupiter it takes longer. So what is being observed as described in this experiment is (time to leave disc + time to contact shadow + time to notice disappearance of light) and what we see is the apparent variation in time to notice the disappearance of light which is due to our distance from Jupiter. The (time to leave disc + time to contact shadow) can be left as one term - we know from mechanics that it is a constant (for any particular geometry) and we are really only interested in the difference between the two observations since this gives us the time difference based on our difference in distance. Now you simply calculate the difference in distance between the two observing positions of the earth (easier said than done as Romer's result shows) and divide it by the distance in total time for each observation.
These days we can calculate our relative positions so much better than Romer could, so we can get far more accurate estimates of the speed of light via his method. However, there are quicker and far more accurate methods of measuring the speed of light thanks to modern technology.
About a year ago, I replicated Romer's experiment using a small telescope. I computed a value for the speed of light that was a bit more accurate than Romer's.
The experiment is described in this blog post:
http://brightstartutors.com/blog/2010/10/25/speedoflight/
An excellent example of the practical use of geometry and astronomy to determine the speed of light.
@MadScientist
The time of actual ending of transit to the the time you observe transit to end will also vary similarly. So, as Dhnice said, the difference between the two, as observed for a single orbit of Io, should be the same.
woww.... amazing.. speed of light now debated...
The light rings around SN1987a also demonstrate that light doesn't go at infinite speed. They appear because light takes slightly longer to travel to the dust that reflects some light towards us from the supernova flash than it took to go the direct route.
TomS,
Variable speed of light theory was proposed by Barry Setterfield primarily based on observations of the speed of light by the US Naval observatory. Setterfield adjusted the Ramer numbers for light speed by correcting with modern values for planetary distances (as he should). With this adjustment, the Ramer data falls within error limits for speed of light in either constant C or Setterfield theories.
The Setterfield assumption is exponential decay to the currently observed value. Extrapolating backwards in time and arriving at at exponential decay based on his data is not justifiable even though a statistically valid fit of the data, as there is no theoretical basis for such a decay and the data is far from being conclusive to justify such as decision. BTW, there are big-bang cosmologists who propose much faster light speed short after the big bang (60 orders of magnitude faster)
I have seen other expositions of Ole Rømer's idea, which present a different reasoning.
My suspicion is that many stories are embellished versions. The general outline of the story is that as seen from the Earth there are anomalies in motion of one of the Jupiter moons, anomalies that are resolved on the assumption that light propagates at a finite speed.
But I see different stories as to which timings are actually used.
Hi Ethan, you present diagrams from Rømer's notebooks. That's very interesting! Original source!
Looking at those diagrams I realize I don't understand them. I've read other versions of the Ole Rømer story, I did understand those stories.
I wonder what Ole Rømer's actual reasoning was. As I understand it, Rømer did not actually perform any calculation. As I understood it from other sources Rømer pointed out the possibility of assuming the Jupiter Moon anomaly arises from finite speed of light propagation.
Interestingly, in the Principia Newton refers to Rømer's hypothesis. In Newton's time it was unknown whether light transmits instantaneously. Newton's favored Rømer's hypothesis.
MadScientist,
Actually, today there are no longer ANY methods for measuring the speed of light. That's because the speed of light is no longer a measured quantity. Effectively, it's a defined quantity.
The definition of a meter is the distance travelled by light in a vacuum in a given fraction of a second. Once we have a definition of a second, the measurement of speed of light really amounts to measurement of a distance.
This occurred because our methods for measuring the speed of light became progressively more accurate. They became so accurate that the main limitation on their accuracy was the definition of the standard meter. Therefore, it makes sense to DEFINE the meter in terms of the speed of light.
Tihomir @16,
Look at the orrery image that's fifth from the end. That corresponds, roughly, to point F on the diagram: the one you're worried about.
It's true that as night falls, i.e., when you're at roughly the 3 o'clock position on the Earth, you cannot see Jupiter. However, as the night goes on, the Earth continues to rotate counterclockwise, and by time you reach the 11 o'clock position, Jupiter rises above the horizon. It will continue to ascend until roughly the 9 o'clock position, when dawn approaches. Remember that even though at any particular instant during the night, you can only see 180 degrees worth of the sky, over the course of the entire night, you can view something more akin to 270-300 degrees. With the exception of when the Earth is very close to position E in Romer's diagram, you will always have a window of time during the night when Jupiter is visible.
@26:
Ethan,
Thanks for the clarification. Of course, you're right. I made a more detailed drawing and came to the same conclusion, wondering why I wasn't able to see it sooner myself. My admirements to Rømer - and you!
Tihomir
"The definition of a meter is the distance travelled by light in a vacuum in a given fraction of a second."
The definition of a second, however, doesn't depend on light except insofar as quantum tunnelling and metastable state radiative relaxation depend on the speed of light.
"The definition of a second, however, doesn't depend on light except insofar..."
It's true that the definition of a second does not depend on the speed of light. (It does depend on the frequency of light emitted by a particular electronic state transition of a cesium atom, though). It cannot depend on the speed of light simply BECAUSE that's how a meter is defined. Consider, if we defined a meter as the distance travelled by light in a given fraction of a second, and then defined a second as the time it takes light to travel a given number of meters, we haven't really defined either of those units.
"It does depend on the frequency of light emitted by a particular electronic state transition of a cesium atom, though"
Which doesn't depend on the speed of it. A 200 Hz signal going at 300m/s is still a 200Hz signal at 400m/s.
"It cannot depend on the speed of light simply BECAUSE that's how a meter is defined."
"It" being the length of a meter. Not the length of a second. The original conversation was: "That's because the speed of light is no longer a measured quantity. Effectively, it's a defined quantity."
Since that statement was then followed with:
"The definition of a meter is the distance travelled by light in a vacuum in a given fraction of a second. Once we have a definition of a second, the measurement of speed of light really amounts to measurement of a distance."
The only way light speed becomes a defined quantity is if the definition of a second is defined by the speed of light.
"Consider, if we defined a meter as the distance travelled by light in a given fraction of a second, and then defined a second as the time it takes light to travel a given number of meters, we haven't really defined either of those units."
Indeed, that would be silly.
Good job that isn't what they do, isn't it.
Wow,
I think we may be talking past each other, but essentially agreeing. Assume a thought experiment in which you can watch a beam of light travel in a vacuum for precisely 1 second. Define "1 second" any way you wish. You then measure the distance travelled by that light in that second.
Remember, we are allowed to define a second in any manner we wish. Let's first define 1 second as some number, x of vibrations of light emitted during such and such a hyperfine transition of a cesium atom, ie. the modern standard definition. We have already defined the meter as the distance travelled by light in 1/300,000,000 seconds, so, by definition, the light travelled 300,000,000 meters. From this data, we would calculate the speed of light to be roughly 300 million meters per second. (I am aware that the real value is slightly less than this, and is more precisely defined)
Let's now define a second in such a way that it is 10 times longer than a standard second. The actual distance travelled by the light is now 10 times greater, but based on our current definitions, we would still state that the light still travelled roughly 300 million meters. That's because we define the term "meter" to mean the distance travelled by light in 1/300,000,000 of a second (again, I am aware that the real definition contains a more precise value). From our data, we again calculate that the speed of light is roughly 300 million meters per second.
This result holds true no matter how we define the second. I am glad you agree with me that it's ridiculous to use the speed of light to define both the meter and the second. But all the same, defining the meter in terms of light speed certainly defines the speed of light all the same. We will get the same numerical value for the speed of light in units of meters per second no matter what definition we use for the second.
To put it more simply, the speed of anything is the ratio of the distance travelled by it to the time needed to travel that distance. So the speed of light is the distance travelled by light divided by the time needed to travel that distance. The modern definition of a meter is that a meter is the distance travelled by light in a given amount of time. Therefore, the modern definition of a meter also give a defined value to the speed of light.
@SpinozaB: "The time of actual ending of transit to the the time you observe transit to end will also vary similarly. So, as Dhnice said, the difference between the two, as observed for a single orbit of Io, should be the same."
No, that is incorrect. Read what I wrote very carefully. Regardless of where you're at, it will take the exact same amount of time for the moon to move away from Jupiter's disc and around and into the shadow. (Seeing the shadow from a distant location such as earth is not the same thing as the object physically plunging into the shadow). From earth you are actually observing an event quite a few minutes in the past and when the earth is at a different position then you are observing with a different time delay. However, the fact remains that it actually takes exactly the same amount of time to move around and into the shadow. And yet if you actually time how long it took for the moon to disappear, you can see that the time appears to vary - that variation is due to the variation in your distance from Jupiter and the transit time of the light.
Look at it this way - imagine you can stand right near Jupiter. To get around the parallax problem at Jupiter, we observe the center of the moon as it passes the edge of the planet and goes around into the shadow. What you observe is an event that takes, say 4 hours. Let's say that it takes exactly 4 hours for the moon's center to cross the disc then plunge into the shadow and from our vantage point near Jupiter we have a delay of only milliseconds between the event and the observation. Now we move far away so that we have a delay of, say, 1 minute in the observations. You now see the center of the moon cross the disc a full minute after the event happened and you expect the center of the disk to plunge into shadow 4 hours after that observed (and already 1 minute delayed) crossing. However, the center of the moon doesn't appear to go into shadow until 4 hours and 1 minute later (a full 2 minutes after the actual physical event). It might sound counterintuitive, but if you write down the equations it's correct.
Oops... I was mistaken in my earlier post. (Dang, only 20 years and my maths is no good.) It is the time on earth at which we expect to observe the occultation which will vary. So SpinozaB is correct - everything is observed with a different time delay but the time between observing the moon cross the disc and observing it going into shadow is the same.
"To put it more simply, the speed of anything is the ratio of the distance travelled by it to the time needed to travel that distance."
Indeed it is.
Have a gold star.
"So the speed of light is the distance travelled by light divided by the time needed to travel that distance."
Yes, this is true.
Two gold stars!
"The modern definition of a meter is that a meter is the distance travelled by light in a given amount of time."
True yet again. Three gold stars!
"Therefore, the modern definition of a meter also give a defined value to the speed of light."
Aaaw. Failed. You were doing so well.
No. You see to get speed you not only need a meter length accurately measured, you also need a second accurately measured.
The second is not defined by the speed of light.
"since 1967, the International System of Measurements bases its unit of time, the second, on the properties of caesium atoms. SI defines the second as 9,192,631,770 cycles of that radiation which corresponds to the transition between two electron spin energy levels of the ground state of the 133Cs atom."
From the wiki entry.
"Let's now define a second in such a way that it is 10 times longer than a standard second."
Why? It isn't a second then, it's a decasecond.
"From this data, we would calculate the speed of light to be roughly 300 million meters per second."
However, since the second is not defined as "How long it takes light to travel 300km", we have not circular reasoning going on.
A cycle of transition takes time, not distance to happen.
"Let's now define a second in such a way that it is 10 times longer than a standard second."
Additionally, you'd have 10x more Cs transition cycles. So light would have travelled 10x longer. Your light speed would then be 3,000 kps as opposed to 300kps. Hence not a constant defined by the definition of second and meter.
Wow,
You're missing the point. The "second" is an arbitrary unit of time. We could theoretically define it any way we wish. If we define what you are calling a decasecond to be a second, then it's a second. A meter is also an arbitrary unit of length. If the SI tomorrow changed the definition of a second to become a duration that is 10x longer than the current definition, then the meter would automatically become a distance that is 10x greater than the distance that is currently defined to be a meter.
The definition of the meter inherently includes the definition of the numerical value for c. c = distance/time. The distance, is certainly 1 meter; that's what the definition of the meter defines. The definition of 1 meter states that 1 meter is the distance travelled by light in a given time, namely 1/300000000 seconds. Therefore, the time is 1/300000000 by definition. 1 meter divided by 1/300000000 seconds is the speed of light and is equal to 300,000,000 meters per second. The fact is that if we change the definition of second, this is still true. The length of a meter, by the modern definition is no longer independent of our definition of a second. Making the second a longer time interval will automatically increase the actual distance that we call a meter in such a way that the numerical value we obtain for the speed of light remains constant.
Re: your post 36,
Given a definition of a second that is 10x longer than its current duration, the light would indeed travel 10x further in terms of actual distance. However, the way we define the unit of distance would have automatically changed at the same time so that the unit we call "meter" would become what we currently would refer to as a decameter. Therefore, even though, in current usage, we would say that the light travels 3,000,000,000 meters, we would have to change our definition of the meter as a result of our new definition of second. Under the new definition of meter, we would have to measure this distance as 300,000,000 meters. That gives a speed of 300,000,000 m/sec just as it was before we changed the definition of second, not the value of 3,000,000,000 m/sec that you state.
I realize that it's tough to grasp that our units are of arbitrary magnitude. However, that's because of common usage for an extended period of time, not because of any inherent physical principal. If we defined the meter in some other way, such as the distance between two marks on a metal bar, for instance, then the speed of light would no longer be a defined value. It would make sense to measure it. If we defined the meter in another way and then defined the second as the time needed for light to travel 300,000,000 meters, we would end up in the same situation we are currently in. That would define c just as the current definition of meter does. The time would then be 1 second, the distance would be 300,000,000 meters, the ratio of the two would be 300,000,000 meters per second.
Wow,
I'm not sure if I'm being unclear with all of this. Maybe think of it this way. Before the current definition of the meter was adopted, the definition of the meter was independent of the definition of the second. At one time, for instance, there was an actual metal bar with two marks on it and the meter was defined as the distance between these marks. That definition was obviously not dependent on the definition of the second. As long as that was true, the speed of light was not a defined value.
The current definition of the meter is that it is the distance travelled by light during a time interval of 1/300,000,000 seconds. That definition is OBVIOUSLY not independent of the definition of the second. Since the length of a meter and the duration of a second are now intertwined, and the factor that intertwines them is the speed of light, the speed of light has a defined value.
Consider an alternate definition of the meter that is dependent on the second but does not utilize the speed of light. Define the meter as the distance travelled by a sound wave of 1 kHz frequency in still air at 760 mm Hg pressure, 0% relative humidity and a temperature of 20C during a time of 1 second. We have just defined the speed of sound in air. The speed of sound in air would then be 1 meter per second. This definition of meter would yield a meter stick that is much larger than what we normally call a meter stick. In fact it would be probably not fit within the borders of some small towns. However, it's a perfectly valid definition.
Wow,
Let me give it one more try:
The Apollo astronauts left a "cat's eye" reflector on the surface of the moon. That reflector allows earth-based scientists to send a laser beam to the moon and have it reflect directly back to their detector on earth. It's possible to measure the time it takes to do so. Dividing twice the distance between the detector and the reflector by the time needed for the laser beam to travel that distance would yield a value for the speed of light.
That begs the question, though: how do you know what the distance between the reflector and the detector is? According to the modern definition of the meter, the distance is determined by multiplying the time needed for this beam to travel to the reflector and back by 300,000,000. Therefore, the distance is 300,000,000t and the speed of light is 300,000,000t divided by t, or simply 300,000,000.
No, the second is not defined as the time needed for light to travel 300,000,000 meters. That's true. A distance of 300,000,000 meters IS defined to be the distance travelled by light in one second. Assume that you can measure 1 second to any arbitrary degree of accuracy you wish. The light then has, by definition, travelled a distance of 300,000,000 meters. There's no point in measuring that distance independently of the time measurement. The measurement of the time has established the distance by definition. If you think you have designed an experiment to measure the speed of light, what you are REALLY doing is a very accurate distance measurement using the primary standard for the meter. That's really what you have done in my prior post, for instance. You have done an accurate measurement of the distance between your laser beam detector and the reflector on the moon.
To measure any arbitrary speed, you are correct; an accurate measurement of both distance and time is needed. However, that's not true for the speed of LIGHT. Light is different because the speed of light is used to define one of the quantities that we are measuring.
"No, the second is not defined as the time needed for light to travel 300,000,000 meters"
Good. Will you keep saying true things, though?
"Assume that you can measure 1 second to any arbitrary degree of accuracy you wish."
Nope. Assume you can measure the time taken for the requisite cycles of the metastable exited state of 133Cs to any accuracy you wish.
Bugger. It didn't take you long to get it all wrong again, did it.
"The light then has, by definition, travelled a distance of 300,000,000 meters."
If you've waited the requisite time for 9,192,631,770 cycles of that radiation which corresponds to the transition between two electron spin energy levels of the ground state of the 133Cs atom, yes.
"There's no point in measuring that distance independently of the time measurement."
There is if you want to find out how long light took to travel any given distance. Light won't have traveled 300 km in 891,453,184 cycles.
"If you think you have designed an experiment to measure the speed of light, what you are REALLY doing is a very accurate distance measurement using the primary standard for the meter."
See, still completely arsed up.
No.
If I've very very accurately measured a distance of 825 furlongs in SI meters, I have found a very accurate measure of distance.
But the time taken for light to cross that distance is required too.
For which you would have to count the number of Cs cycles and divide by the number of those in one second.
You can then deduce that light goes at some speed.
If all you know is the distance light went, then you haven't worked out the speed of light.
"an accurate measurement of both distance and time is needed. However, that's not true for the speed of LIGHT."
Yes it is.
You measure a very accurate distance.
Then you need the time to travel that distance for light.
In a refractive medium this will not be the same as light speed in vacuuo.
Or is your contention that light moves at 300kps in water, say?
"Light is different because the speed of light is used to define one of the quantities that we are measuring."
Yes. But it isn't used to define the other.
Therefore if you decide the unit of time (the second) will be a rounder 1,000,000,000 cycles you will find that your speed of light is (approximately) 32.6kps.
So your speed of light figure is different if the interval of one second changes.
"That begs the question, though: how do you know what the distance between the reflector and the detector is?"
Nope, it doesn't. "It's possible to measure the time it takes to do so." isn't why they put that mirror up there.
And that is answered anyway. How many cycles of Cs occur between you sending a light pulse and you getting that light pulse back.
This, however, is the definition of the meter.
Not the definition of time. And not the definition of the speed of light.
Light speed depends on the definition of the second.
Since that second depends on something that isn't based on the speed of light, we don't have, as you perspicaciously pointed out, a case where:
"if we defined a meter as the distance travelled by light in a given fraction of a second, and then defined a second as the time it takes light to travel a given number of meters, we haven't really defined either of those units."
"The length of a meter, by the modern definition is no longer independent of our definition of a second."
It is.
One depends on light traveling, one depends on an electric field oscillation at a single point.
Your problem here is that you've got your knickers COMPLETELY in a twist with:
"1 meter divided by 1/300000000 seconds is the speed of light and is equal to 300,000,000 meters per second."
The fact is that that was because it gave a meter that was very close to the one defined earlier which was a bar of metal.
If we used a time interval of 1/10,000 a sidereal day we would have a different divisor defining the meter.
"However, the way we define the unit of distance would have automatically changed at the same time so that the unit we call "meter" would become what we currently would refer to as a decameter."
Nope, we'd use a divisor that was 10x larger.
Our meter would still be around 39 inches long. The speed of light would be 10x higher too.
I'm not sure what else I can do to explain this, so I'll take one last shot and then I'm done. You can have the last word if you want.
What you are saying is true for an arbitrary measurement of velocity. It's not true when what you are measuring the velocity of is light.
It IS pointless to measure both the time taken by a beam of light to travel a certain distance and independently measure that distance. Let's say you do so anyway. Let's say you measure the time as 1 second and then you independently measure the distance as 350,000,000 meters. You have not proven that the speed of light is 350,000,000 meters. All you have proven is that your independent measurement is wrong. How do I know it's wrong. Simple. The distance travelled by light in 1 second is DEFINED to be 300,000,000 meters. Any measurement that gives another number is wrong.
Sean, you're still completely wrong.
What happens when another significant digit is put on end of the speed of light figure? Do we redo all our meters and recalculate all our clocks?
NO.
We change the speed of light.
"Simple. The distance travelled by light in 1 second is DEFINED to be 300,000,000 meters."
Yes. This defines a meter.
It doesn't define a second.
You see velocity is written down in meters per second.
You need both.
http://en.wikipedia.org/wiki/Speed_of_light#Increased_accuracy_of_c_and…
"Because the previous definition was deemed inadequate for the needs of various experiments, the 17th CGPM in 1983 decided to redefine the metre."
So it wasn't to keep the speed of light absolutely in the median.
"Improved experimental techniques do not affect the value of the speed of light in SI units, but do result in a more precise realization of the metre."
But not of the second.
If we'd defined a second differently, we'd have defined the meter differently, just like we redefined the inch to be 2.51cm. That doesn't mean we changed the duration of a second.
To be absolutely clear:
ME: What happens when another significant digit is put on end of the speed of light figure? Do we redo all our meters and recalculate all our clocks?
YOU: They redefined the meter!!!!
If, for example, they find an actual reason why their determination of the speed of light is incorrect (maybe finding that the mechanism they took to define the light speed in vacuuo was incorrect, they'd pick a different figure. Just like the speed of light went from
299,792,456.2±1.1 m/s.
to
299,792,458 m/s
which is outside the error bars of the MEASUREMENT.
Why? To make a better accord with what measurements they could manage and had already made on other SI units. I.e.. they picked a WHOLE number of Cs cycles rather than fractional to fit.
So we changed the speed of light so that we could define the meter.
We didn't change the speed of light to refit the definition of the second.
If you don't believe me or the wiki site, then maybe some other sites will convince you:
"The metre is the length of the path travelled by light in vacuum during a time interval of 1/299 792 458 of a second.
This defines the speed of light in vacuum to be exactly 299,792,458 m/s." From http://math.ucr.edu/home/baez/physics/Relativity/SpeedOfLight/speed_of_…
or from http://physics.nist.gov/cgi-bin/cuu/Value?c
speed of light in vacuum
Value 299 792 458 m s-1
Standard uncertainty (exact)
Relative standard uncertainty (exact)
Concise form 299 792 458 m s-1
Wow,
I'm done. take it up with the NIST (The US government agency charged with maintaining standards of measurements)
from http://physics.nist.gov/cgi-bin/cuu/Value?c
speed of light in vacuum
Value 299 792 458 m s-1
Standard uncertainty (exact)
Relative standard uncertainty (exact)
Concise form 299 792 458 m s-1
In case you don't get the significance of the NIST information, the only values that are exact are values that are DEFINED. Measured values always have some uncertainty. NIST certainly thinks that the speed of light has been defined. I'm inclined to trust their thoughts.
Sean, the problem here may well be that you haven't thought through your concerns properly.
1) If the second had been significantly different, they would have used a different definition of the meter. Therefore your assertion is 100% absolutely and definitely WRONG on large differences in the prior definitions of both the meter and the second.
2) Metrology is about the PRACTICAL measurement of quantities. Therefore if something better than "the distance light goes over a second" comes up to measure linear distance, THIS WILL BE USED.
Additionally, currently the most accurate measure we have involved here is time. The meter was less well defined, basically being "the length of this stick here". Weight (being dependent on volume) increases the accuracy needed for linear distance and may have been the reason for the change of the "speed of light" that you insist would never be done.
Measuring the distance light goes in a set time is more accurate than "the length of this stick here", so they used it. But if the tolerances they need mean they can't change the length of a meter when they get higher accuracy on that distance light travelled means that they will, if needs be, change the definition of the meter by the length light travels in a second to a different figure.
Remember: they changed the speed of light once. They can do so again.
They haven't just said "the speed of light is this AND WILL NEVER CHANGE". They've defined the second accurately and can measure it to great precision. They've measured the distance light travels in a set time to great precision. The tolerances needed for the meter allowed them to pick a whole number of meters in the definition of distance by that traveled by light in a second.
But you see as far as metrology is concerned, both time and distance are continuous.
That means that at least one of the trifecta is incorrect. Either time needs to be a non-even number of Cs cycles, in which case they could define it as a different transition or stress the Cs to change the frequency of the cycles produced, or change the speed of light, or change the definition of a meter.
They did that once. It was easier to redefine the speed of light the first time to set the length of a meter. In a subsequent change, it was easier to change the length of a meter and keep the speed of light as defined. And to date, it's not acceptable to change the speed of light because we have measuring devices to whom that change would be noticed.
But there's no reason why they'd change the meter again next time.
Your assertion in that light speed is defined and the meter depends on that is correct. Your assertion that this means that the speed of light CANNOT change is wrong.
Wow,
You just knocked down a straw man. I NEVER said that light speed could not be changed. All I said was that the CURRENT definition of the meter also defines the CURRENT value of light speed. Since the particular fraction of a second used in the definition is an arbitrary one, certainly if it made practical sense to do so, it could be changed and light speed would have a different value if that happened. Maybe I wasn't clear in my discussion of this. In all of my posts, I was simply stating that defining the meter in the way that it is currently defined also at the same time defines the speed of light. I never intended to suggest that this definition is immutable for all time.
I think we are in full agreement then. If you measure the time taken for a beam of light to travel from point A to point B, then absent a redefinition of the meter, all you have really done is measured the distance between points A and B, because (again, absent a change in the definition of a meter) this distance is DEFINED in terms of the travel time of the light beam.
"I NEVER said that light speed could not be changed."
cf:
"25
MadScientist,
Actually, today there are no longer ANY methods for measuring the speed of light. That's because the speed of light is no longer a measured quantity. Effectively, it's a defined quantity."
That's your first post.
In your scenario, the speed of light is still defined. When I say the speed of light is defined, I mean it's value is set by the unit definitions as opposed to experimentally determined. Even if the numerical value for the fraction of a second that is specified in the definition of the meter is changed (which is equivalent to changing the numerical value of the speed of light), light speed is still defined and not an experimentally determined quantity.
I'm not sure why you think that to say something is "defined" means that it cannot change. For example, the meter has always been a defined distance. Whether it's been defined as a fraction of the circumference of the earth, the distance between two scratches on a metal bar, a multiple of the wavelength of the light emitted during a specific electronic transition of a particular atom, or as a distance travelled by light during a specified fraction of a second, it's still a defined quantity. Similarly, the speed of light is defined. If it's found to be useful in the future to redefine the meter in some way other than as the distance travelled by light in some specified time period, then the speed of light will no longer be defined.
I am going to stop arguing with you here (and this time I REALLY mean it). I am doing so because I think our differences on the matter at this point are more a result of misunderstandings due to imperfections of language and/or our respective inability to properly express ourselves in it. (Probably more so on my part than yours). Thanks for the lively discussion.
> In your scenario, the speed of light is still defined
Nope.
If, for example, they find a better method of defining length (say the length of X carbon atoms in a nanotube regular solid), then that will be used because it doesn't rely on another measure (time), like I said. You need time defined as well as measure distance light traveled.
"I'm not sure why you think that to say something is "defined" means that it cannot change."
I'm not sure why you think that's what you said:
"Actually, today there are no longer ANY methods for measuring the speed of light."
and
"That's because the speed of light is no longer a measured quantity."
Since these refute the option of the speed of light being anything other than a set figure like "2".
You definitely CAN measure the speed of light. And if a more acceptable method to measure a set invariant distance is possible, then this will be done.
As it was done once already.
WoW is 100% correct. The distance covered per unit time. You can use arbitrarily define the meter and the second, but the fact remains that the total distance covered in a certain time is the same. If you define the meter as x Hz and the second y Hz, and you take a piece of string and make it as long as the distance it travels in a given interval of time, it doesn't matter what the f*****g units are, the length of the string is the same, whether the second is defined by the interval between x number of oscillations of a butterfly's wings or a quantum logic clock, as long as the time interval is the same.
Changing the definitions of meter or second, no matter where you get them - even from light itself - does not impact the absolute distance covered per absolute interval of time.
The accuracies can be refined, the string length is the same whether you call it 300,000,000m/s, or 186,000M/s, or 3cutirbs/whufflesnuff.
You can define your meter any way you want, you can say your length of string is 3.01x10^8 meters, or 2.89x10^8 meters, it is still the same length.
While on the subject of Rømer, maybe a post on thermometers next?
Or on /why/ he was working on observations of Jupiter's moons?
(He did it in order to find out where Tycho Brahe's observatory on Ven was in relation to the observatory in Paris. The latitudes were not that hard to measure but the longitudes were pretty hard, given the state of the art of their clocks. The observations had something to do with that.)
earth- sun roughly 150.000.000 km. which makes circumference about 2 x pi x earth-sun. . It takes 42.5h for Io orbit Jupiter. Earth travels at most 2.677.493km a day around the sun and approximately x (42.5/24h) = 4.741.395 km away from Jupiter-Io before the next immersion or emergence. Speed of light 300.000km/s makes that light takes 15seconds longer before observed on earth.
I canât see other reasonable explanations for Io's observed time difference from earth.
15 seconds delay could easily be detected in the course of 42.5/24 days because pendulum clocks were widely available in western europe at the time of Rømers experiment.
But if predictions of Ioâs emergence /immersion time were calculated in advance and written on a calendar we easily get to a difference in minutes over the timespan of a year. Taking into account that pendulum clocks were accurate enough at that point in history.
I think we are in full agreement then. If you measure the time taken for a beam of light to travel from point A to point B, then absent a redefinition of the meter, all you have really done is measured the distance between points A and B, because (again, absent a change in the definition of a meter) this distance is DEFINED in terms of the travel time of the light beam.