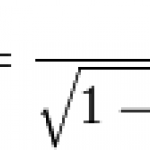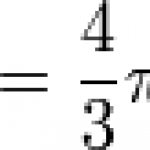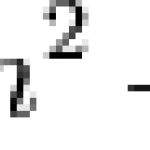Sunday Function
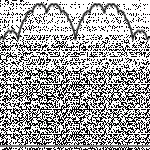
I think we've developed a nice theme over the last few weeks, gradually working our way through a less well-behaved function - the triangle wave - and trying to find various series expansions for it. "Well-behaved" is kind of a term of art, which mathematicians use as shorthand for long strings of caveats about differentiability and continuity and which physicists use because who wants to memorize those long strings?
Well, to some extent we have to. While it's not very common that badly-behaved functions arise in physics, there are functions which at least don't always remember to say…
Sorry for the two-day delay. The personal business to which I alluded kept me out until yesterday morning, delaying this post until today. I hope it's decent for all that!
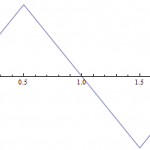
This week, the same function as last week. There's nothing so special about the function itself, but it does serve as a nice Rorschach blot to project our own wandering mathematical thoughts upon. As with last time, the specific "f(x) = stuff" form of the function is not particularly enlightening. It's just a few lines tacked together. The graph is all we need.
Last time we set ourselves the task of writing this…
There's an interesting book I'm working on called The Fall of Rome: And the End of Civilization, by historian Brian Ward-Perkins. He argues (against a prominent modern school of thought) that Rome did indeed fall rather than merely change, and that European civilization really was wrecked pretty hard with a recovery that by many fairly objective numerical metrics took almost a thousand years to reach its former level of economic complexity and living standards. It wasn't a fast and sharp break separating the Roman from post-Roman world, but it was in fact a break.
You can make a similar…
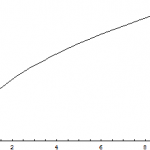
All right ladies and gentlemen, take out your calculators. Punch in the number 4. Whack the square root button. What do you get?
Unless I am badly mistaken, you're going to get the number 2. As you probably remember, the square of a number is just that number multiplied by itself: 3 squared gives 9, 4 squared gives 16, 1/2 squared gives 1/4, etc. The square root is the inverse of this process. It tells you what you have to square to get the given number. Two times two is four, so the square root of four is 2. You can plot the graph of the function to see what the square roots of…
You know what's gonna happen? I'll tell you what's gonna happen. Troops are now forming behind the line of trees. When they come out, they'll be under enemy long-range artillery fire. Solid shot. Percussion. Every gun they have. Troops will come out under fire with more than a mile to walk. And still, within the open field, among the range of aimed muskets. They'll be slowed by that fence out there, and the formation - what's left of it - will begin to come apart. When they cross that road, they'll be under short-range artillery. Canister fire. Thousands of little bits of shrapnel wiping the…
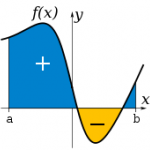
We've done a lot of discussion of the concept of integrals of a function here on this blog. Their definitions and applications are so broad as to defy any one-sentence description, but one of the most basic is the idea of the area under a curve. More precisely it's the signed area under the curve - that is, the area above the x-axis is counted as positive and the area under counts as negative. Stealing the image from Wikipedia, which communicates the concept well:
In some cases you might have a function that exhibits a particular kind of symmetry about the origin. On one side of the…
Last week we did the sinc function. Let's do it again!
The function, to refresh our collective memory, is this:
Now I was thinking about jumping right into some contour integration, but on actually doing it again I see that it's a little hardcore for one post so eventually when we do it we'll have to stretch it out over probably three posts. Probably it'll be a Friday-Saturday thing culminating on an official Sunday Function. But it ain't gonna be this week. This week we're going to do three ways of computing a limit. There's more, a bunch more, but we're going to just do three.
As we…
I first met this function sometime in the year 2001 in the manual for a graphing calculator. The manual said that the function had no "closed-form analytic antiderivative" but nonetheless the calculator could integrate it numerically. At the time I had no idea what any of that meant, but upon taking a high school calculus class I met the function again as a demonstration of the concept of a limit. In my freshman calculus class in college I met the it yet again and learned that while this function and all continuous functions have an antiderivative, the antiderivative can't always be…
I've been away from campus visiting family during the first part of the summer, in one of those rare confluences of events where research, classes, and teaching all find themselves on temporary hiatus. While it's pretty rare, I'm glad to take it. It is giving me Mathematica withdrawals though, especially with being able to easily make nice graphical plots and do some of the number-crunching I sometimes need for the more technical posts around here. Fortunately this is the last Sunday I'll have that problem, as I'll be back in Texas soon (and all those responsibilities will come roaring…
If you want to kill some time, try to think of all the different definitions of the word "set". You have chess sets, sets in tennis, sets of dishes, sets musicians play, sets as abstract mathematical entities, television sets. You can set a table, set a clock, set someone straight, set a price, set out on a journey. That's just scratching the surface. The Oxford English Dictionary lists literally hundreds of different senses of the word. And yet if I set out (ha!) a particular instance of the word, you'll process its meaning instantly.
You'd think mathematics could avoid the ambiguity…
Saw "Up" yesterday. How Pixar manages to be so consistent in their astonishing quality is entirely beyond me. In a bit of a tribute, this Sunday Function is not about any dramatically important special function, but instead it's about filling a balloon. Air or water, as your preference.
You'll have noticed that when you start to fill a balloon, its radius expands very rapidly at first before slowing dramatically. A water balloon will go from 1 to 2 inches much faster than it will go from 6 to 7 inches. Why? Because if you fill the balloon at a constant rate, you're increasing the…
Just 24 light-hours away it's still Sunday, right? Oh well. On to the math!
If you ask a mathematician to define a circle, you'll probably hear something along the lines of "A circle is the set of points in a plane equidistant from a given center point. The name of the distance from the center is the radius." A mathematician will state it more precisely, but that's the gist. As a technical matter - and mathematicians love technical matters - this is actually somewhat different from what kids learn about circles in school. Kids would probably say a frisbee is a circle, but really it's…
Nobody ever asks the interesting questions at presidential press conferences. But if somehow I could choose a question, it would be this:
"Mr. President, has the NSA solved the integer factorization problem?"
Of course it's unlikely he'd know off the top of his head, and even if he did he certainly wouldn't give me an answer. That's the kind of codebreaking knowledge that quickly becomes useless if everyone knows you know. Large chunks of modern cryptography are based on the fact that it's easy to multiply numbers like 17863 * 8161 = 145779943. But given a number like 223233911, it's a…
Pick a two-digit number. Anything from 0 to 99 inclusive will work, because the single digit numbers can be considered to have a leading zero. Add the digits together. Subtract that from the original number. So if you started with 12, you add the digits to get 3, and subtract that from 12 to get 9 as your final answer.
Ok well that's a bit mundane and boring, though it sounds like the setup to a magic trick. And so it is. We'll worry about the trick in a minute. First we'd like to write that algorithm as a function. First we'll have to figure out a way to extract the digits from the…
Let's do two functions today. As sometimes happens, in this case we're not so interested in the functions themselves as the fact that these functions happen to be part of a general class of functions. Just as we can classify the real numbers as even, odd, or neither (numbers like pi, 1/2, and the rest of the non-integers are neither), we can classify functions as odd, even, or neither. This is a random even function and its graph:
What makes this function even? A function is even if it's symmetric about the y-axis. In other words an even function will have the same value at at x = 1 as…
"So," Herr Schrodinger says to us, "I'm looking for a function of x. It needs to be equal to the negative of its second derivative, up to a constant factor. When x is zero, the function itself should be zero. And when x equals L for some constant L greater than zero, the function also needs to be zero. Can you find me such a function?"
Sure we can. As you know, the derivative of a function is its rate of change. Its second derivative is the rate of change of the rate of change. There are functions which are equal to their derivative (and second derivative), e^x is one of them. But we'…
The quadratic formula. With the exception of the Pythagorean Theorem, it's probably the single most common mathematical formula people carry from high school. It's not a function as such, it's something that solves a function. Let me give an example:
Pick a number x, square it, add twice x to that, subtract 3 from that. You might want to figure out what x makes the answer equal to zero. It's the kind of thing we have to do in physics all the time. In this case, the answers (and you can find them by several methods) happen to be -3 and 1. Plug them in and you'll see that you end up…
Well, it's Gabriel, Gabriel playin'!
Gabriel, Gabriel sayin'
"Will you be ready to go
When I blow my horn?"
- Cole Porter, Anything Goes
The commenters in last week's Sunday Function proposed an excellent idea for this week. As we did then, we'll start simple and work up to it. Graph the curve f(x) = 1/x.
Now take the horizontal axis and think of it as an axle, one that can rotate smoothly. Hook a motor onto it and spin it up to a nice fast clip. The graph of the function will trace out a surface in three-dimensional space. In the business, we call it a surface of revolution. It looks…
Let's start with a pretty simple function. It's not this week's official Sunday Function, but we'll use it to get there.
Take the number 1, divide it by x. Pretty easy. Now imagine putting a dot at the point x = 1 on the x axis, and draw a line straight up from there to the curve formed by the graph of the function. Then do the same thing for another point on the x axis (with x > 1). Shade in the area in between the lines. Ok, that might be a little hard to visualize if you've never done it before. Let me pick the other number to be x = 4, and I'll actually put the picture below…
A tricky one:
At x = 2, f(x) = 1 + 2 + 4 + 8 + ...
Which, uh, is clearly not going to end anywhere finite. The series fails the single most basic necessary (but not sufficient) condition for convergence of infinite sums - that the terms of the series approach zero as you go farther and farther up the chain of addition.
On the other hand, f(x) is equally clearly not divergent for all x.
For instance, at x = 0, f(x) = 1 + 0 + 0 + ... = 1
So that's a start. Maybe there's other numbers x can equal where the series has a finite value. What are they? This is one of those problems where it's…