"It's a wonderful world. You can't go backwards. You're always moving forward. It's the wonderful part about life. And that's terrific." -Harvey Fierstein
Yes, it's true. As stationary and secure as it seems when you plant your feet firmly on the ground, the reality is we are always moving through the cosmos.
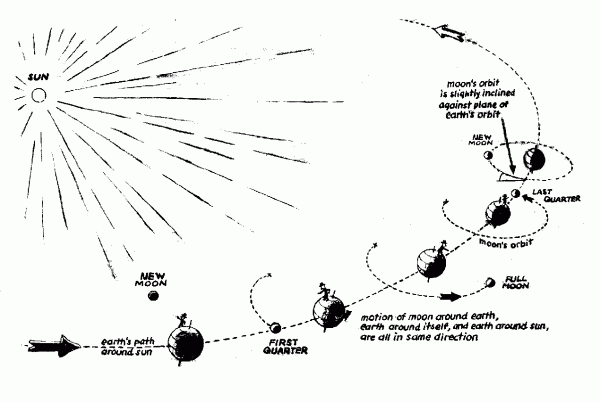 Image credit: H.A. Rey, via Samuel J. Wormley of http://www.edu-observatory.org/.
Image credit: H.A. Rey, via Samuel J. Wormley of http://www.edu-observatory.org/.
About its axis, the Earth spins around once per day. Unless you're at the exact north or south pole of the planet, that means that you are in motion, too! The fastest-moving among us are located at the equator, moving just over 1,000 miles-per-hour (1,600 km/hr), decreasing steadily as you move farther away in latitude. (Just north of the 45th parallel, where I am, I move at about 700 miles-per-hour, or just over 1,100 km/hr.)
But regardless of where you are on Earth, we're all moving faster than that.
Orbiting around the Sun annually, we traverse a giant, nearly-circular ellipse some 584 million miles (942 million km) in circumference. (Or, for an ellipse, in perimeter.) That comes out to a speed of 67,000 miles-per-hour (107,000 km/hr). In fact, that's so fast that it makes more sense to talk about miles (or kilometers) per second rather than per hour: 18.5 miles-per-second or 30 km/s!
But it's not like the Sun is a stationary object, either.
Located some 25,000 light-years from the galactic center, the Sun speeds through our gigantic Milky Way along with the vast majority of other stars in our vicinity, making an elliptical-shaped, wobbly orbit. The last time the Sun was in this location relative to the Milky Way, reptiles and primitive dinosaurs dominated the Earth; it was some 225 million years ago in the Triassic period. Since our Sun was formed, we've made about 20 trips around the Milky Way, moving at a mean speed of about 137 miles-per-second (220 km/s).
So you're moving along with the rotating surface of the Earth, flying through space around the Sun, all while the entire Solar System speeds around the galaxy. But is the galaxy itself moving?
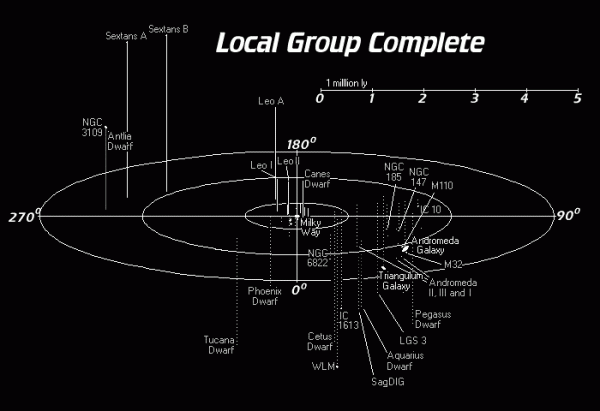 Image credit: Moravian College Astronomy, via Star Watch at http://www.astronomy.org/.
Image credit: Moravian College Astronomy, via Star Watch at http://www.astronomy.org/.
More importantly, how would we know?
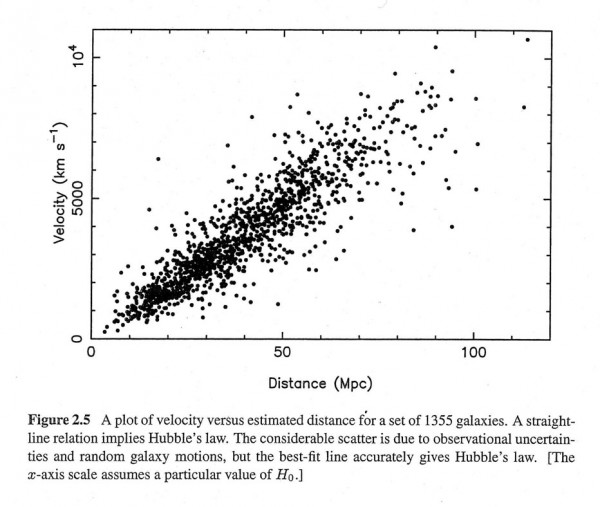
You might think to look at the galaxies all around us. After all, you know that the Universe is expanding, and that the galaxies farther away from us are moving away faster and faster from us, directly proportional to their distance. It's a great idea, and a fantastic thing to try.
Unfortunately, it won't work.
You see, the expansion of the Universe is by far the dominant effect on how fast objects are moving away from us on large scales, but on smaller scales, gravity can be very important. The gravitational effects from a large galaxy cluster or supercluster can cause a galaxy to move by hundreds or even thousands of kilometers-per-second different from what Hubble's law predicts.
This is well understood and expected, and is known as an object's peculiar velocity. Since our Universe is very clumpy and clustered, we'd expect our galaxy to have a peculiar motion, too. But even if we were successfully able to map out the nearby Universe, that wouldn't tell us what our own peculiar motion is.
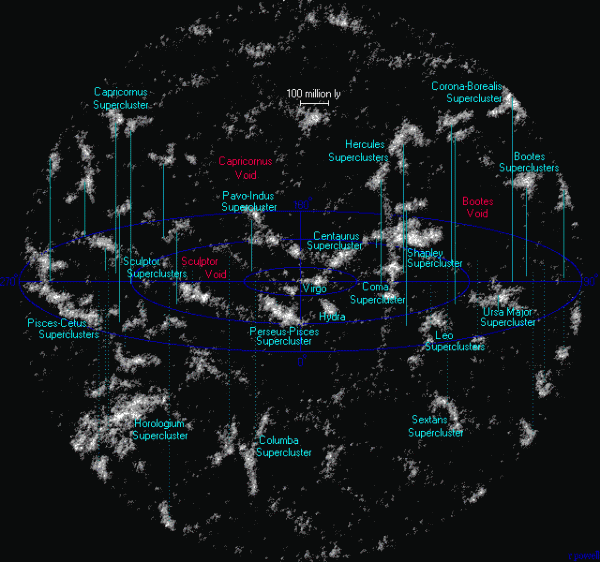 Image credit: Richard Powell of http://www.atlasoftheuniverse.com/.
Image credit: Richard Powell of http://www.atlasoftheuniverse.com/.
But there is a way to measure this, and we owe a great debt of thanks to the Cosmic Microwave Background for allowing us to do this!
About 380,000 years after the Big Bang, neutral atoms formed in the Universe for the first time, making it transparent to all the radiation left over from the Big Bang. That radiation then travels in a straight line for all eternity, stretching in wavelength as the Universe expands, until it runs into something.
Well, we're something, and so when we look in any direction in space, we see this leftover radiation with the same exact energy spectrum and temperature: about 2.725 Kelvin.
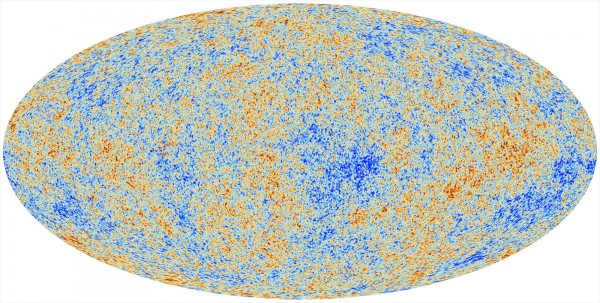
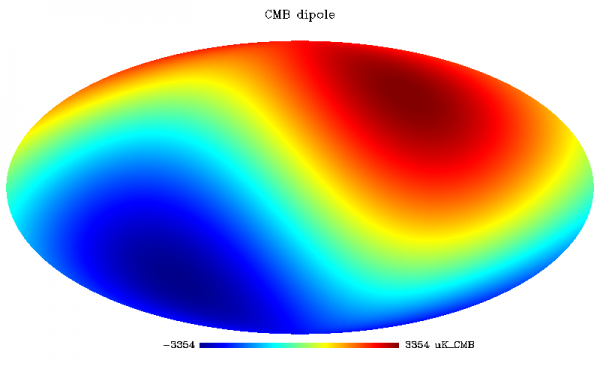
The thing is, this isn't exactly what the microwave sky looks like. Last week, I gave you five facts you probably don't know about the Cosmic Microwave Background, but here's one more. You've probably seen this now-famous picture of the microwave sky as seen by the Planck satellite.
This shows you the fluctuations about the mean temperature that we observe in the Cosmic Microwave background. Of course, you have to take away the mean temperature to show this; these are fluctuations on the order of tens to hundreds of microKelvin, as compared with the background temperature that's tens of thousands of times greater in magnitude. But there's something else that needs to be subtracted out: a directional red-and-blueshift caused by our own motion relative to the background radiation itself!
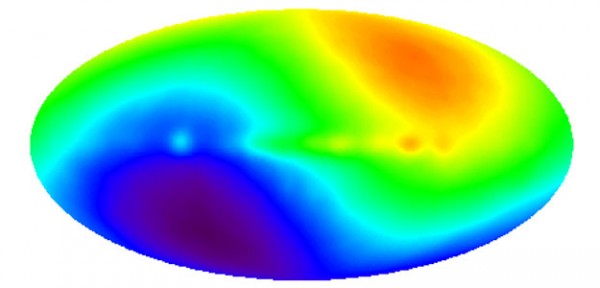
There's a direction in the sky that the background radiation is redshifted by a maximum of about 3.3 milliKelvin, and 180 degrees away from that in the opposite direction, the radiation is blueshifted by the exact same amount. There are only two explanations: either the entire Universe is moving with respect to our galaxy by this amount, or it's our galaxy that's moving relative to this radiation. Given everything we know about physics, relativity, and the observed relative motion of every other galaxy in the Universe, we can be pretty confident that it's the latter.
This corresponds to a speed of about 670 km/s, or 416 miles-per-second; just over 0.2% the speed of light. This is a totally typical and reasonable peculiar velocity, although it's fair to say that we are uncertain as to what gravitational structure is causing it. (About 20 years ago, people assumed it was a mass known as the great attractor; that appears now to be ruled out as the cause of our peculiar motion.)
You may also notice that this dipole -- in spherical harmonics, this is known as l = 1 -- is omitted from all graphs of the cosmic microwave background's temperature fluctuations.
That's because it has to be subtracted out, and if it were on the graph, it'd be a factor of thousands larger than all other points here. This is a little frustrating, because there actually is a primordial dipole (l = 1) component to the cosmic microwave background's fluctuations, but we are unable to measure it because of our own peculiar motion. In fact, if we're at all imperfect in subtracting it out, it could artificially lower the quadrupole moment, something which was heatedly discussed in the community about a decade ago.
Thanks a lot, gravity!
Although it doesn't look like -- thanks to dark energy -- we'll ever merge with any other galaxies beyond our local group, the presence of these distant masses continues to effect us gravitationally, and alter our motions through the cosmos. How great it is that here we are to see it!




Great post
@Ethan -- Thank you very much for this detailed discussion of the CMB dipole, our proper motion, and the fact that I completely failed the orders-of-magnitude seminar in my previous comment ;-/
On a side note, I have to ask -- do Rocky and Eugenio *really* think our Universe is expanding ellipsoidally, or was that just their art department's flub?
I have an important question for you, is it the case that most of galaxies out there have the shape of a disk, I mean stars are distributed in two dimensions? and if so; what determines the axis of a disc-shaped galaxy?
I am fascinated with the idea that there is a cosmic rest frame, a privileged inertial frame. The CMB dipole is evidence of a cosmic-global property ... so is it just a statistical global property or is it a local property of space? Ie, does our galaxy considered in isolation have an absolute motion?
For instance, does composition of large (relative to c) velocities actually work according to special relativity? Is it really transitive and associative, or might there be distortion? Is there some way to tell?
@Mina Kamel #3: You may be interested in the Wikipedia article http://en.wikipedia.org/wiki/Galaxy_morphological_classification. Not all galaxies are disk shaped: "elliptical galaxies" range from spherical to football (rugby ball)-shaped blobs of stars. The "spiral" (disklike) galaxies also have significant variations. When there is a disk, its formation is driven the same way that solar system's become planar: if an initial spherical distribution of matter is rotating, then as it collapses under gravity that rotation will increase, from conservation of angular momentum. A fast-rotating body is most stable with its mass flat in the plane perpendicular to the rotation.
@Marshall #4: The CMB rest frame is *not* "privileged" in the relativistic sense. It is merely the frame of reference at which all of the motion of stuff in the Universe averages out to zero (or equivalently, the frame of all the matter in the universe from before it clumped up and started developing local motions).
No object "considered in isolation" can have an absolute linear motion. Motion is measurable only relative to some baseline. The CMB frame provides a very nice baseline against which all observers can agree.
The composition of velocities in special relativity is easily measurable in the laboratory. In my field, particle physics, short-lived particles are produced in collisions travelling at very high velocities. When those particles decay, their daughters are also travelling at high velocities, and so on through sometimes three or four stages. Our ability to both measure and predict these processes is completely dependent upon relativistic kinematics, which is therefore extremely well tested.
It is merely the frame of reference at which all of the motion of stuff in the Universe averages out to zero (or equivalently, the frame of all the matter in the universe from before it clumped up and started developing local motions).
Can you break this down further in caveman language. I'm having a hard time understanding what that means.
@ Michael Kelsey #5 There was another part of @ Mina Kamel #3 question I believe that maybe you can still clarify, "what determines the axis of a disc-shaped galaxy." My search to understand this turned up wikipedia anisotropy stating: "Cosmic anisotropy has also been seen in the alignment of galaxies' rotation axes."
Perhaps you, or of course Ethan, can elaborate. Thank you.
@crd2 #6: I presented two different ways to think about what the "CMB rest frame" (or the "CMB dipole") means physically.
The first model I described as, "the frame of reference in which all of the motion of stuff in the Universe averages out to zero." Suppose that you're omniscient. You pull out your perfect spectrographic telescope and you measure the full 3D motion of every big object (galaxy or larger) in the visible universe. You also measure their distances perfectly, so you can subtract away the Hubble motion (cosmological expansion) of all those objects. Now you have a long list of motion vectors relative to us. If you add up all those vectors, you have the _net_ motion "of the Universe relative to us," or equivalently, our motion relative to the whole rest of the Universe (on average). That's what the CMB dipole is telling us.
The second version, "the frame of all the matter in the Universe before it clumped up," is just describing the CMB directly. At the time of last scattering (when the CMB photons stopped being absorbed and scattered by ions) the Universe was extremely close to just being a uniform, isotropic gas. No galaxies, no giant black holes, no nothing. Just a whole mess of gas, with the atoms zipping around randomly at a temperature around 3000 K.
Without structure, that whole Universal volume of gas was (by definition) at rest with respect to itself. Since then, the matter in the Universe has clumped up to form galaxies, clusters, and whatnot; the gravity between those objects caused them to move around locally (galaxies orbit one another, clusters collide, etc.). In this model, the CMB dipole tells us how our particular clump happens to be moving with respect to the original featureless gas.
"There are only two explanations: either the entire Universe is moving with respect to our galaxy by this amount, or it’s our galaxy that’s moving relative to this radiation."
I feel as though these are equivalent statements. At least today, if not in the past (i.e. what led to the motion or which thing was accelerated). Michael Kelsey's explanation in #8 furthers this belief. Is there some way in which these aren't equivalent, now?
Similarly, this makes me wonder if we need to (or can) find something now that's "causing" this motion. It's motion, not acceleration, right? So something had to cause it, but that could have happened billions of years ago, and I imagine it'd be nearly impossible to wind the clock back with enough detail to figure it out now. I mean, I assume the CMB photons being red- and blue-shifted in opposite directions would tend to exert a net braking force on any object interacting with them, but I also assume that that effect is negligible, even when summed over billions of years. (Not to mention the net force drops as the relative velocity does, so it's never likely to reduce motion to zero.)
Not really, Ben. Thinking so is how you get the Twins Paradox with Special Relativity.
Given your quoting there, why, though, did you stop there? Did this bit:
"Given everything we know about physics, relativity, and the observed relative motion of every other galaxy in the Universe, we can be pretty confident that it’s the latter."
Not make you think twice? Or did you genuinely not see it?
@Roy #7 (my long reply #8 appears after your post because yours was still caught in moderation when I wrote mine, so I never saw it): What determines the axis of rotation of galaxies? Our best understanding (and Ethan can explicate the supporting evidence better than I possibly could) is that it's essentially random.
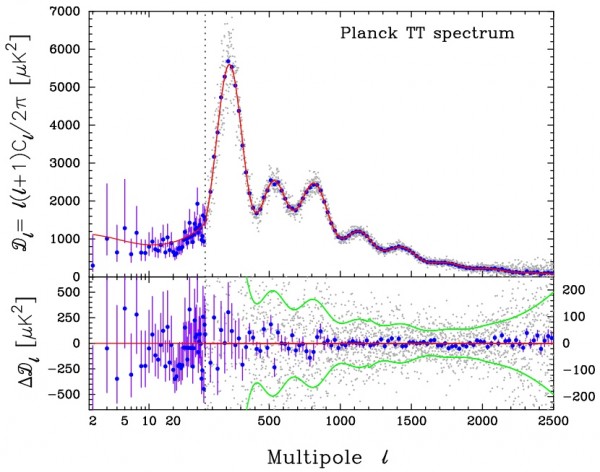
The "evidence" for a large scale alignment of CMB multipoles (the so-called "Axis of Evil" cited in your Wikipedia link) is basically that one data point (at l=2) at the far lower left of Ethan's final plot, above. The claim is that the axis of that quadrupole moment lines up with the axis of our own motion (the dipole), whereas it "shouldn't line up" if everything were random. This is, as you might expect, a rather extraordinary and contentious claim. "Random" most certainly doesn't force anything to be _not_ aligned (consider the constellations, which are explicitly human pareidolia imposed on a random distribution); having two multipoles out of hundreds happen to line up is certainly no evidence for non-randomness.
The followup sentence you quoted, regarding alignment of galaxies' rotation axes, is stated in the article without citation. The articles I have read on the subject have seemed rather fuzzy to me; the statistical evidence for large-scale alignments are marginal at best. Also, I would expect there to be a significant selection bias in terms of needing the axis of rotation to be "close-ish" to perpendicular to our line of sight just so we can get a decent handle on the Doppler broadening due to the rotation (a face-on galaxy would have no measurable rotational Doppler).
So what *does* determine a rotation axis? The environment in which the collapsing clump of matter finds itself. Once you start having local or regional clumping of matter, then on those scales things are no longer homogeneous or isotropic (you have a clump over here, but not over there; you have a big clump off this way, but just a little clump way yonder). So the blob you're considering experiences different gravitational pulls, and different tidal torques, from different directions. Those will, over a long enough time, induce some net rotation, and as the clump collapses further, that rotation will be amplified just from conservation of angular momentum.
If a larger, collapsing clump fragments into pieces (for example, the presolar nebula collapsing to a dusty disk and a protostar, followed by that dusty disk forming planets), then you would expect those _pieces_ to have somewhat correlated alignment axes. Since the larger system started with some angular momentum, as it fragments that momentum will be shared among the pieces. The energy cost for having one of those piece flip its axis is quite large, and so is unlikely unless some catastrophic interaction (collision, merger, etc.) provides the necessary energy input.
Another nice article, Ethan. Pity though that the expansion illustration features galaxies on the surface of a balloon rather than the raisins in the cake. That might have got us into something really interesting: does the universe have an edge? There's a howling non-sequitur that can be found on even very reputable websites, to the effect that space is flat hence the universe must be infinite. Phooey! One for another day perhaps.
Okay, another question. According to Ned Wrights tutorial, the question was asked " How can the universe be infinite if it was concentrated into a single point at the Big Bang"? His answer " The entire universe was not concentrated into a single point, but the observable universe was concentrated into a single point. Huh? This doesn't make sense. Either the universe is the entirety or merely a part of a whole.
Sorry, is this 20 questions, and what are we playing to win?
Why does the universe have to be infinite?
@John Duffield #12: I don't understand why you call that a non sequitur; can you provide a citation?
A truly _flat_ (identically zero curvature) spacetime is necessarily not closed (in order to close, some part must have positive curvature). Therefore, a truly flat spacetime is either bounded with an edge, or unbounded and therefore infinite. If all you're saying is that we don't have data to choose between those alternatives, then you're correct.
The original point of inflation was to provide a mechanism by which an actually closed, curved spacetime could _appear_ flat to us (as our own Universe seems to), because we occupied such a small piece of the whole. Obviously, we have discovered in the subsequent 40-ish years that inflation has much more going for it than just solving the flatness problem.
@Michael Kelsey #15, @John Duffield #12 is correct in saying that spacetime can be flat, finite and have no boundary. The simplest case is the three dimensional torus.
Intuitively these three criteria would seem to require curvature but that is only because our intuition tries to construct such a closed universe "floating" within our own flat space, in which case you need to twist it around to get all its edges joined up.
The 2D torus is easier to visualise. Consider a flat square such that if you move along the square and reach a side "edge" you just reappear on the opposite side and continue moving. This is a (2D) flat finite space with no boundary. If you curve it around and glue the "edges" together you get the more familiar shape of (the surface of) a doughnut, which is a torus *with* curvature.
Well point of fact John Duffield didn't say spacetime can be flat, finite, and boundaryless. Rather they suggested that it can be flat, finite, and therefore have a boundary. Apparently because the raisin bread anology suggests it because bread has an edge. Which is a bit like saying that the baloon anology suggests the univese has a nozzle.
@ 13 Tony
Our observable universe is not the whole of the Universe. Not by a long shot. There is nothing strange or weird about that. We are limited by the speed of light and passage of time. There are stars and galaxies out there that we will never ever observe. If you want an analogy.. maybe think of a fish in a pond. It can never ever observe all of the planet earth. Some things are just outside of it's range of observation.
As for observable universe vs whole and single point, again correct. We know how big our observable region is.. you know.. 14BLy x 2 plus expansion.. think it's around 80or something billion lightyears.... turn the clock backwards..13 billion years and you get a point.. or some small scale.. like 10^-50 or something.... But you are still left with the rest of unobservable universe which again shrinks.. but in some other points.. all over.. we don't know how big that was, because we don't know how big the whole Universe is. I think it's safe to say we'll never know. On the other hand.. the space at the edges of our observable universe is moving away from our point faster than speed of light. Thus in effect, our observable universe is all there is for us. But it's not all of the Universe.
@Ray Hindle #16: I'm still confused, Ray. Probably because I'm an experimental physicist, and neither a theorist nor a mathematician.
It's not the "embedding" that confuses me, it's the object itself. If you want a space with a periodic coordinate, without some non-physical "teleportation" to get the periodicity, then I think you _have_ to have non-zero, positive curvature along that axis.
If you can point me to a (hopefully understandable!) citation that explains otherwise, I would really appreciate it.
"Which is a bit like saying that the baloon anology suggests the univese has a nozzle."
And will eventually be turned into a humorous rubber Giraffe later on...
@Michael Kinsey #19:Trying to visualise non-Euclidean spaces *is* difficult :) A Wikipedia entry for the 2D flat torus is here: http://en.wikipedia.org/wiki/Torus#Flat_torus
and the principle applies exactly the same as for a 3D flat torus (but with less mind bending).
I think you still need to consider the problem of trying to mentally embed the flat finite no-boundary space into a visualisation within our 3D flat space because that is the cause of the confusion. The flat torus simply can't be visualised that way.
I put "edges" in quotation marks because they aren't really edges (and there is no teleportation). The "edges" are actually joined to opposite "edges", but this join can't be represented in flat 3D space, so they just represent a way of trying to conveniently visualise the torus.
Consider a chess board with squares numbered by the usual a1 to h8 system. For example e5 is adjacent to d4,e4,f4,d5,f5,d6,e6 and f6 so a king on e5 can move to any of these 8 squares. Now suppose we use the chessboard as if it were a 2D torus. Then the squares adjacent to a1 for example are (in the same order) h8,a8,b8,h1,b1,h2, a2,b2. If you were a king and you lived in this universe to could move to any of these 8 squares. And you would see your universe as flat finite and without boundary.
It's like the problem of visualising the shape of space near a black hole or when walking into the TARDIS. One can't, or at least I can't.
Michael,
I think the problem you might be having is that the term "curvature" doesn't necessarily mean what it does in vernacular terms. It has a very precise mathematical definition, more akin to something like "noneuclidean-ness", if that makes any sense. For instance, consider the earth's surface (assuming it's a sphere for simplicity). Just as one example, you can draw a triangle on the earth's surface which has the sum of its angles greater than 180 degrees. (consider two points on the equator and the north pole, for instance). That shows that this surface is mathematically curved.
Now, surfaces such as a torus or a cylinder appear to us to be curved surfaces in vernacular terms. However, in mathematical terms cylinders and tori are flat surfaces. This can be seen simply from topological considerations. You can take a cylinder, cut along a line parallel to its axis, and unwrap it to form a flat plane, all without tearing the surface. (Think of it in reverse, take a sheet of paper and roll it up to form a cylinder. You can do so without tearing the paper.) Simiarly for a torus, cut through the torus and unwrap it to make a cylinder. We already saw that the cylinder is flat. (Again with the paper analogy, roll it to form a cylinder, then join the two ends to make your torus.)
These surfaces are manifestly Euclidean, since you can "unroll" them into a flat plane. We simply define lines, etc. as we do in Euclidean geometry, but transformed by the "rolling up" process. Thus, a triangle on a plane gets transformed into a triangle on a cylinder. The "rolling up" process preserves the angles between the lines, so we still have a Euclidean triangle with a sum of angles of 180 degrees.
so... Reddit is also discussing this.. my old-man attitude is that the universe is bounded and finite. but people are always pointing out to me that Lambda equals one and that means the universe is flat and if it is flat it is infinite.
Is there anyway that it is flat locally but curved on really huge scales?
or can a flat universe be bounded and therefor finite? (or does it work the other way? finite first and then bounded..?)
nasa re WMAP: "We now know (as of 2013) that the universe is flat with only a 0.4% margin of error. This suggests that the Universe is infinite in extent; however, since the Universe has a finite age, we can only observe a finite volume of the Universe"
"Is there anyway that it is flat locally but curved on really huge scales? "
Absolutely. We can only know the universe is flat by measuring, and our measurements have error bars. I recall Ethan had an article on that very subject. Oh hey google found it:
http://scienceblogs.com/startswithabang/2012/07/18/how-big-is-the-entir…
@Michael Kelsey #15, re "I don’t understand why you call that a non sequitur; can you provide a citation?" There's plenty of websites such as http://map.gsfc.nasa.gov/universe/uni_shape.html which say things like "We now know (as of 2013) that the universe is flat with only a 0.4% margin of error. This suggests that the Universe is infinite in extent". Also see http://en.wikipedia.org/wiki/Shape_of_the_Universe#Global_geometry . Or see http://www.astro.ucla.edu/~wright/cosmology_faq.html#RB which says "So we know empirically that the volume of the Universe is more than 20 times bigger than volume of the observable Universe". Or see http://www.esa.int/Our_Activities/Space_Science/Is_the_Universe_finite_… where you can read "So you have two possibilities for a flat Universe: one infinite, like a plane, and one finite, like a torus, which is also flat". See CB's link and note what Ethan said: "we know that the entire Universe extends for at least 14 trillion light years in diameter".
I can't give you a citation for the non-sequitur however. That's me saying that. On a very large scale energy density is uniform and space is homogeneous. So expansion apart, light doesn't curve, there's no overall gravity, no overall curvature, and the universe is flat. Not nearly flat, flat. But it is expanding, and it can't be expanding if the "pressure" is counterbalanced at all locations. So it can't be infinite. So it has to be something like a ball. For an analogy think of a droplet of water. Waves within the droplet undergo total internal reflection. This option simply doesn't feature in the given alternatives. And from what I know of fundamental physics and relativity and Einstein's greatest blunder, it's the right option.
@Ray Hinde #16: as CB said, I meant a flat finite universe with no instrinsic curvature. See http://arxiv.org/pdf/1303.5086v1.pdf where the Planck collaboration reported no evidence for a torus.
@Sinisa, In other words the entire universe did not spring from the same Big Bang inflaton model?
No, the entire universe is more than our visible universe. It came from the same Big Bang event and nothing SL said implies it didn't.
"Is there anyway that it is flat locally but curved on really huge scales?"
The earth.
Looks flat to me, well, if I'm on a river plain or on a large body of water it does.
But people know the earth in its entirety is spherical.
@ 27 Tony
No, all of the Universe underwent inflation. But it already had "some" size. Then, every single quanta of that space inflated to sizes that far surpass what our observable universe is.
Singularity universe, which what you imagine as starting from a single point just can't work. That's why inflation was invented in the first place.
Kevin Dowd,
See my post above. A flat universe can indeed be bounded. A torus for instance, despite how it appears to us, is a flat surface that is obviously bounded. To really understand this, consider a 2-torus, ie. a typical donut in our familiar 3 spatial dimensions. Now, intrinsic curvature is mathematically the deviation from our Euclidean geometry that we learned in school. Imagine a 2-D creature living on a piece of paper. His world is obviously flat. Now, unbeknownst to our 2-D critter, who can't perceive a third spatial dimension, we roll that piece of paper into a cylinder. Assume that our critter is the 2D version of Euclid; he's developed a geometry relevant to his flat universe. How would this geometry change after we roll up the paper? Remeber, he can't perceive the third dimension, so his geometry does not change. Now, to complete the analogy, roll up the cylinder so that the open ends are joined together, and you get a 2-torus, which again would not appear any different in terms of the geometry to our 2D Euclid. Therefore, the 2-torus is a flat surface.
Ethan -thanks for your posts - I enjoy them greatly - and the comments are an education unto themselves. Also enjoy your avatars - are you a Burner? If not, you should go - you'd be a hit!