Quantum Erasure

When I posted congratulating the winner of this year's Nobel betting pool, I received a gentle reminder in email that I'm a Bad Person and still haven't done one of the posts I owe to the 2011 winners. Evan reminded me that he asked for something about the delayed-choice quantum eraser, so let's talk about that a bit, in the traditional Q&A format.

So, what's a delayed choice quantum eraser do? It may or may not have rubbed out mistakes you made while writing, but you don't know until later when somebody else chooses to read it? Nothing physical gets erased. The delayed-choice quantum eraser is all about information. Specifically, it's an experiment that shows the weird influence of measurement on quantum mechanics.

So what's that got to do with choosing to erase things? The idea is that you can alter the character of a measurement by arranging to be able to know certain things, and then again by "erasing" that information. And weirder still, you can make the decision about whether to do the erasing "after the fact."

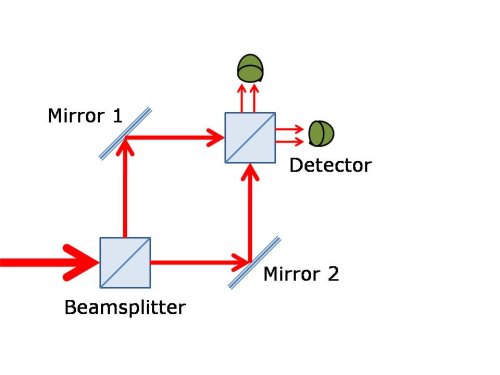
"Arranging to be able to know certain things" sounds awfully weaselly, dude. I mean, either you know them or not. This will go more smoothly with a concrete example. The quantum eraser requires some sort of interference experiment; there's a really nice Scientific American article on how to make one that takes a double-slit sort of experiment as the starting point, but I prefer to think about a Mach-Zehnder interferometer, which looks like this:

A Mach-Zehnder interferometer.

A beam of light comes in from the left, and hits a beamsplitter that sends half of it up, and passes the other half straight through. Each beam hits a mirror that directs it to a second beamsplitter, where the beams are recombined. Half of the initially reflected beam gets reflected again, and half of the initially transmitted beam gets transmitted again, and those pieces fall on the detector at the top. The other half of each beam gets sent to the detector at the right.

This seems like a really complicated way to get half of the light to each detector, dude. That's what it seems like at first glance-- each detector sees half of the light from each of the two possible paths through the device, and each path started with half of the initial light, so you end up with half the total light at each detector.

But this ignores the fact that light has wave nature. When you add the light from the different paths, you're adding waves, and the result of that is very different. If the two paths are the same length, the peaks of the wave that took the upper path fall on top of the peaks of the wave that took the lower path, and they combine to make a really big wave at the detector on the right-- if you do the math out, you get 100% of the incoming light at the detector. If you make one path a little bit longer than the other, though, the light traveling along that path takes a little longer to reach the detector, and if the delay is just right, the peaks of the wave traveling the long path are delayed a bit, and end up falling in the valleys of the other wave. In which case, you get nothing at all.

So, when the path lengths are equal, you get twice as much light as you put in? 100% at each detector? No, when they're equal, you get 100% at the right detector and nothing at the upper detector. This is because there's a phase shift of the light when it reflects off a beamsplitter, that also moves the peaks. The detector at the right sees two beams that have each experienced one reflection and one transmission, so they're the same, but the top detector sees one beam that was transmitted twice and one that was reflected twice. This delayed the twice-reflected wave by exactly the amount needed to put peaks into valleys, so with equal paths you get nothing.

And as you change the path, what happens? If you slowly lengthen one of the paths, you go from 100% at the right detector and 0% at the top to 0% at right and 100% at the top, then back. Over and over. If you measure the amount of light on each detector as you change the path length, they trace out two sinusoidal curves, 180 degrees out of phase with each other.

Okay, sounds good. But nothing's getting erased, here. No, not yet. The next step is to "tag" the two paths, by using a polarizing beamsplitter for the first step. If you do that, you still get 50% of the incoming light reflected and 50% transmitted, but now the two are distinct. The 50% that gets reflected is vertically polarized, and the 50% that gets transmitted is horizontally polarized. Then you use a non-polarizing beamsplitter for the second step, and when you add the waves back together, you get...?

Ummm... Pretty rainbow patterns? No, you get 50% of the light at each detector, no matter what you do to the path lengths.

So you've erased the pattern! Quantum is weird! No, there's actually nothing quantum about this. You can explain it perfectly well as a classical wave phenomenon-- you're adding together one wave with vertical polarization and another with horizontal polarization, and that will never give you an intensity variation.

So nothing changes at all? There's still a change, but it's harder to detect. What you would see is a change in the polarization-- when the peaks of he two waves coincide you get polarization at a 45 degree angle from the vertical, and when the peaks of one fall in the valleys of the other, you get a polarization at 45 degrees in the other direction from vertical. Midway between those, you get circular polarization. But the overall intensity is always the same, so the signal from your detectors doesn't change.

So, how do you make this quantum? Well, you use a really, really weak light source. Like, one photon at a time weak.

With a really weak light source, you know that you're sending a single, particle-like quantum of light into the device at any given time. And you will detect a single photon at one of the two detectors at the other end of the apparatus. But if you repeat this many many times with different path lengths, you'll see an interference pattern without photon tagging-- 100% of the photons at one detector and 0% at the other, then the reverse at a different path length. And when you use polarization to tag the photons, you just get 50% at each, no matter the length.

The language people usually use to talk about this is that the polarization tagging makes the two paths distinguishable. If you measured the polarization of the photon at the detector to be vertical, you would know that it took the top path, and if it's horizontal, you know it took the bottom path. This means that the photon behaved like a particle, taking only one path, and thus doesn't show any interference effect.

And that's quantum erasing? The pattern goes away when you tag the paths? No, that's the step before the eraser. It's just minimally quantum when you're dealing with single photons. The "erasing" in the quantum eraser is an erasing of the tag.

What you do to make an eraser is to put a polarizer in front of your detector that's at a 45 degree angle to the vertical. This has an equal probability of passing the vertically polarized photon that took the top path and the horizontally polarized photon that took the bottom path, which means they're no longer distinguishable. And when you do that, you get the interference back-- the probability of seeing a photon at a given detector oscillates between 100% and 0% as you change the length of a path.

The traditional language to describe this is that you've "erased" the path information. Since you can no longer distinguish the paths, the photon behaves like a wave, and takes both paths, giving you interference.

Wow. Quantum is weird. Yes and no. This is col, but in another sense, it's not really a surprise. Because remember what I said earlier-- adding together classical waves with orthogonal polarizations doesn't give you an intensity variation, but does give you a change in polarization.

Looked at that way, the recovery of the variation can be explained classically: with equal path lengths, you have 45 degree polarization in one direction, which goes through your polarizer with 100% probability. Make one path a bit longer, and you have circular polarization, which has a 50% probability of getting through. Make that path still longer, and you get polarization at 45 degrees the other way, which is blocked by the polarizer. And so on.

So, wait, if you can do this all classically, why do people talk about this stupid thing at all? Well, again, if you're using single photons it's sort of minimally quantum-- you know you've sent in a single particle-like excitation, but you're seeing wave behavior indicating that it took both paths. That's quantum.

Things don't really get weird and impossible to explain classically until you add the delayed-choice part.

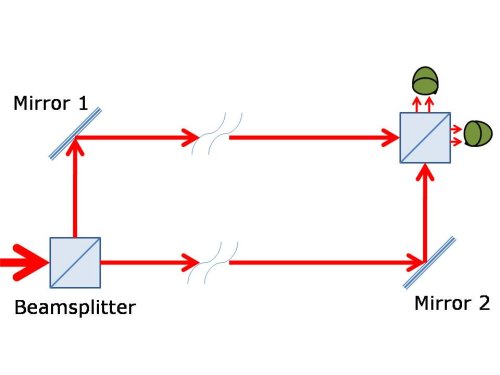
And what's that? Well, you set up your interferometer with polarization tagging, but you make it really big:

A really long Mach-Zehnder interferometer.

And rather than putting a polarizer in front of the detector and just leaving it there, you use something like an electro-optic modulator that can switch between acting like a 45 degree polarizer and acting like a block of plain glass very rapidly. Then you send one photon at a time into your interferometer, and switch the settings of the detector very rapidly. If you look at just the runs of the experiment when you had the modulator in the "block of glass" setting, you'll see 50% of the photons regardless of path length. If you look instead at the runs where you had the modulator set up to act like a polarizer, you'll see an interference pattern as you change the path length.

But you can understand those classically. Rigt, but here's the weird part: You make the decision about which sort of detector to use after the photon has passed the first beamsplitter.

Huh? Well, you can't literally do that, because you can't track a photon that well, but in principle, that's the idea. If you know exactly when your source spits out one photon, and you know the speed of light, you pick your final detector setting at a point in the experiment when the time until you expect the photon to arrive at the detector is less than the time required for light to travel from the first beamsplitter to the detector. In that case, the photon must have been "in flight" in the experiment before the decision about what to detect was made.

So, the interference pattern goes away? Nope. When the detector is set where you expect to see interference, you see interference, and when it's set to not see it, you don't.

Whoa. Exactly.

So, how do you explain that? Classically, you can't. In quantum terms there are a bunch of ways to talk about this, depending on what interpretation you prefer. In a collapse type interpretation, you're making a change of the wavefunction. In a Many-Worlds type interpretation, you've just selected which "universe" you're in-- all of the possible outcomes exist as pieces of the universal wavefunction, but at the time of measurement, you "pick" just one of those possible outcomes. A Bohmian sort of interpretation would always have the particle taking a definite path, but the change of detector settings produces an instantaneous, non-local change in the guiding potential that determines the specific path, and steers the photon appropriately. And so on.

Whichever of these you favor, though, the result is undeniably weird.

Photons are strange. Yep. Though it should be noted that this isn't specific to photons-- you could, in principle, do the same thing with electrons, or atoms, or molecules. Anything with two distinct internal states could be used, provided you have a way to selectively "tag" one of the two. I don't think anybody's done it with material objects yet, though there are proposals for doing just that, and it's only a matter of time.

And that would be cooler in some way? Well, in the sense that matter waves are more inherently weird and quantum than light waves, yes. It would also be cleaner in some sense-- one of the objections you sometimes hear when people talk about this is that you can't really define the position of a photon in flight, so you can't actually say with certainty when it has passed the first beamsplitter for the purposes of timing your detector switching.

Material objects have a clearer limit on their speed, so in that sense you can more properly talk about a position within the experiment and that sort of thing. But then, I suppose that slow speed might open some kind of wacky information transmission loophole, so maybe it wouldn't be any better.

This whole business kind of makes my head spin. Good. That's how you can tell it's really quantum physics.