I exchanged a bunch of emails a week or two ago with a journalist who was working on a story involving the possibility of faster-than-light travel. He wanted me to check some statements about the relationship between FTL and causality. FTL creates problems for causality, because if you have an object moving faster than light, there will be pairs of observers who see events involving the FTL object happening in different orders, which means somebody will see an effect happen before its cause.
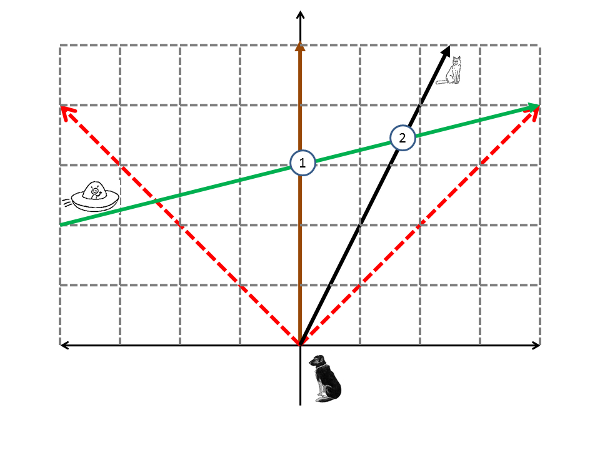
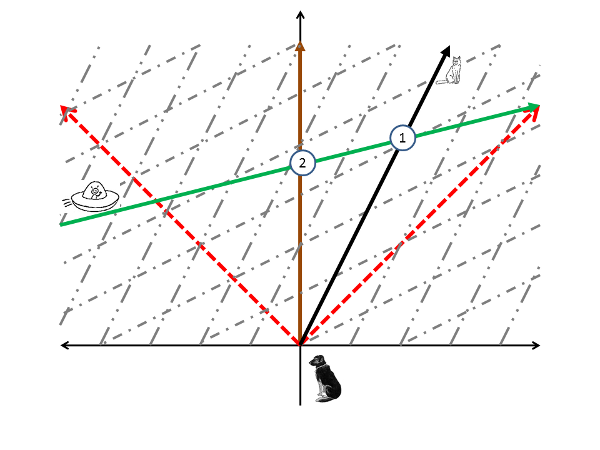
I talk about this is How to Teach Relativity to Your Dog using the example of a stationary dog, a moving cat, and an alien zipping by at four times the speed of light. Here's a figure showing how this appears to the dog:
A dog and cat interacting with an FTL alien, as seen by the dog.
In this "spacetime diagram," the left-right axis indicates the position along the direction of the cat's motion, while time marches upward into the future. Vertical lines are equally spaced position markers according to the dog, while horizontal lines are equally space instants of time according to the dog. The dashed red lines are rays of light sent out at the instant the cat and dog had the same position, and set the scale for everything.
The dog sees the cat moving left to right at half the speed of light. The alien comes in from the left, passes the dog first (event 1), and then the cat (event 2). Perfectly sensible, and the dog could, for example, hand the passing alien a water balloon which the alien could then use to soak that pesky cat.
This looks very different if you replace the dog's grid of position and time markers with the cat's, though. In that case, you get something that looks like this:
A dog and cat interacting with an FTL alien, as seen by the cat.
Both space and time look different to the cat, due to her high speed. Equally spaced position markers according to the cat have to tip to the right, parallel to the cat's trajectory, while the cat's time instants tip up. The regular squares of the dog's grid become rhombuses in this representation.
According to the cat, then, the alien passes the cat, and only later passes the dog. Which makes the whole water balloon thing kind of problematic-- the alien would appear to the cat to come in from the right empty-handed, soak the cat with a water balloon and then carry that balloon on to the left, and later on hand it to the dog.
This reversal of ordering obviously screws up causality, and is one of the best reasons why FTL travel is impossible. It's even possible to create paradoxes by using FTL communications, so sending information faster than the speed of light is ruled out.
My journalist friend had this basically correct, but we went back and forth a bit about a subtle issue of perception. This is always a tricky business in relativity, as it's very tempting to attribute weird effects to the finite travel time for light to get from one place to another, and say things like "The events according to the cat appear to be in the opposite order." That's not what's really going on, though-- relativity isn't about optical illusions. There is no measurement the cat can do that will tell her anything other than that the alien passed her first, and only later encountered the dog.
I think we got this cleared up-- I don't think the story has appeared yet, which is also why I'm being coy about the identity of the journalist, who is free to identify himself in comments. But it did raise the question in my mind of what this would actually look like from the point of view of the dog. That is, what would the dog see?
You see, the diagrams above are a sort of "God's eye" view of the scenario, not the kind of thing any of the participants could directly record. The dog could draw this diagram of events, but only after the fact, after either compiling the records of lots of individual observers at the different position markers, or by looking at the light she sees, and working backwards to correct for the travel time of the light emitted by different objects.
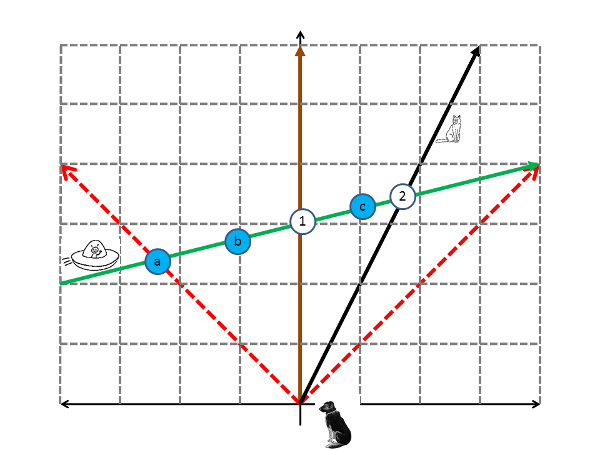
So, what would the "dog's eye" view of the scenario really look like? How would the dog perceive her interaction with the alien? Well, we can understand this by adding some extra events to the diagram:
A dog and cat interacting with an FTL alien, as seen by the dog, with extra events added.
Here, I've added events "a," "b," and "c," so there are two events on either side-- while the alien is approaching, and while the alien is heading away. To work out what the dog sees, we need to add lines corresponding to the light emitted by the alien as it passes each of these. Looking at the approaching side first, we see that things are a little weird:
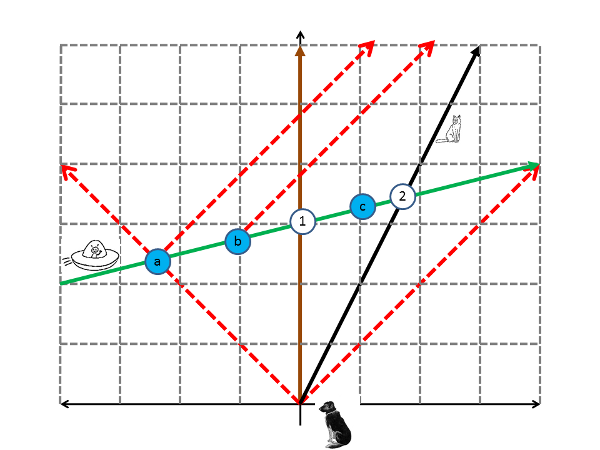A dog and cat interacting with an FTL alien, as seen by the dog, showing the light from the approaching alien.
The alien, moving at four times the speed of light, arrives well ahead of the light from earlier in its trajectory. Thus, the dog would have absolutely no warning of the alien's approach-- it would just suddenly be there. Then the light from nearby would arrive (event b), and then the light from farther away (event a). If we add in the receding side, we have:
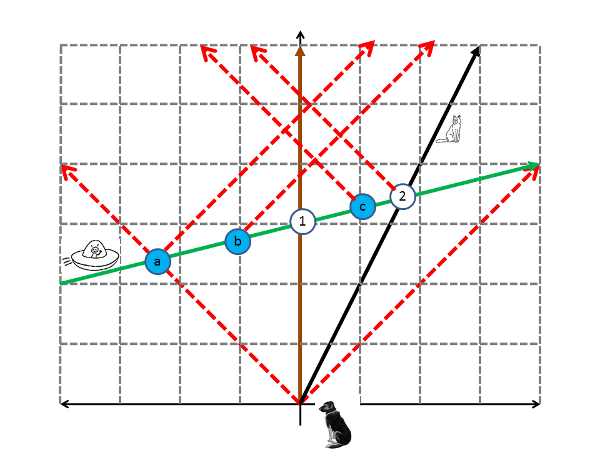A dog and cat interacting with an FTL alien, as seen by the dog, showing the light from the alien as it approaches and recedes.
Again, the alien outraces its own light, so it's gone just as suddenly as it appears. The light from its departure lags well behind the actual events, with nearby events appearing only after some delay (event c) and more distant events much later (event 2, the soaking of the cat).
So, the answer to the question "What does the dog see?" is "Some weird stuff." Adding markers for the arrival of the light from each of the events gives you the idea:
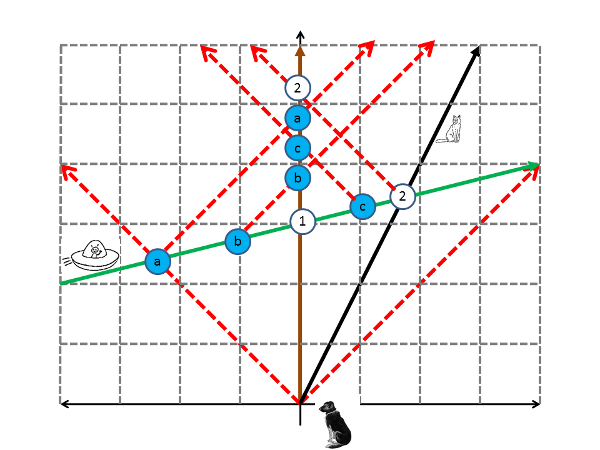A dog and cat interacting with an FTL alien, as seen by the dog, showing the order of events as seen by the dog.
From the dog's point of view, the alien appears without warning (event 1), then seems to move away in both directions simultaneously-- like two identical aliens headed in opposite directions. Light from a given distance on the approaching side will arrive a bit ahead of light from the receding side (event b is seen before event c, though they're the same distance away), so it will look sort of like the alien zipping off to the left is heading away a bit faster than the one heading off to the right. The "dog's eye" sequence of events is not the "a-b-1-c-2" sequence of the "God's eye" view, but "1-b-c-a-2." It's only after the fact, when she's had time to say "What the hell was that?" and do a bit of math that the dog can construct the global picture shown in the diagrams.
So, there's the answer. You could extend this to the cat's scenario by a similar process of event-adding and line-drawing, but I'm not going to. We'll call that homework-- draw and label your diagrams neatly, and send them to Rhett for grading.
And don't even think about moving faster than the speed of light. Seriously, it'll mess with your head.
- Log in to post comments
More like this
I'll come out as the journalist you refer to. I don't think my issue was thinking of relativity as an illusion, but how to explain it without giving this impression. And your post is a great example of how to do so.
Thus, the dog would have absolutely no warning of the alien’s approach– it would just suddenly be there.
This resembles the lies-to-children explanation for why shock waves develop in fluids containing objects moving supersonically: the presence of a moving object in the fluid would normally be transmitted to other locations by sound waves, and of course that can't happen if the object is outrunning its sound waves. Weird things do happen at shocks, like discontinuous changes in density and flow speed (and magnetic field, if the fluid in question is a magnetized plasma). Of course, in fluid mechanics there are other ways to transmit information, so a Mach number greater than one is not a sufficient condition to create a shock. For example, current thinking is that the interface between the Sun's magnetic field and the interstellar medium does not produce a bow shock. That's why this explanation is a lie-to-children in fluid mechanics. But in this scenario, any alternate way of transmitting information would not be any faster than photons, so this explanation might actually be correct, or would be if the scenario were allowed.
I remember doing something similar after learning about Lorentz transforms. Being a total nerd I had a Tardis instantaneously jump to a departing USS Enterprise at 0.9c. Then jump back instantaneously using the Enterprise frame of reference and finding I had traveled back before I left. Just showed up there's no such thing as "at the same time" when FLT is involved.
I wrote an article about faster-than-light travel for a Swedish popular science magazine last year. Unfortunately, it only appeared online in Swedish. (I think I sent an English version to George at some point.) I didn't go into these details though as my point was mainly to say there are different ways to allow faster than light travel. (Hit me over the head. We're all slightly nuts in quantum gravity, I know.) Your post would have made the perfect primer :)
If we observed an object actually crossing close to our path faster than the local speed of light, we would presumably look very closely at whatever happened to space-time close to the object for whatever new physics we might see. Fortunately the dog [and the cat] would see it appear before it passed the cat [the dog], so both get a (fleeting) chance to start the camera to record any weird physical effects. Something moving as you have it doesn't preclude /local/ Lorentz invariance (hopefully in 3+1 dimensions the alien's path doesn't actually intersect with the paths of either dog or cat; I certainly wouldn't want to be too close but please may I have a towel).
i think that is paradox existing only on the einstain TR ground (i mean that on the newton theory ground nothing happen or not??)maybe that vanishing when we found ultimate theory ? but back to story if dog give alien water ballon that he easy found right sequence events no matter how he be tangled that be always way to found right sequence alien come-i give him water ballon-alien gone
The problem getting the causality issues across may be just with saying things like "someone will *see* effects happening before their causes."
To my mind, that's not really the problem at all; the big problem is, as you briefly mentioned, backward-in-time communication: the way that, if Lorentz invariance holds, you must be able to string a couple of these things together to have effects happen inside the cause's own past light cone. That's what induces all the associated causal paradoxes (unless some hackish out intervenes, as some have proposed).
Hi Chad,
Something similar to your explanation of what the dog sees---an alien appearing out of nowhere, and then basically two copies of the alien flying off in opposite directions---is similar to a picture Feynman invoked when discussing various implications of relativity for quantum mechanics. The combination of relativity and quantum mechanics famously leads to the prediction of antiparticles. I won't go into all the details here, but you can think of the spontaneous creation of a particle/antiparticle pair as essentially what is going on with the alien from your dog's perspective. Let's suppose that instead of flying away, the "two" aliens were to then come back and converge on the dog and then disappear (as spontaneously as they appeared) once they have fully re-converged, you'd basically have the annihilation event. If you draw the spacetime diagram, what you'll see is that the alien worldline is a circle in spacetime! This is the picture Feynman proposed for thinking about particle/antiparticle creation and annihilation.
Naturally, one has to think very carefully about how to make such a picture fully consistent and their are many subtleties.
So, what does it look like from the perspective of the alien?
So the alien is like particle that spontaneously appears and then decays into a pair of particle/antiparticle?
There are some superficial similarities between the appearance of a faster-than-light object as seen in the light arriving from it at the position of a particular observer. It's important to remember the distinction between what you see and what's really happening, though.
That is, in the case of the FTL alien, the dog sees two aliens pop into existence from nowhere and zoom off, one of them moving backwards, but that's an optical illusion. After the fact, she can work backwards and show that it was really a single alien moving at FTL speed.
The cat would see something similar when looking at the light from the alien, but again, would be able to reconstruct the trajectory of a single alien rather than a mysterious pair. she would disagree with the dog about the direction of the alien's motion, though. Neither cat nor dog, however, will ever be able to do a reconstruction showing that there were two aliens present at the same instant at different locations in space.
In the case of a particle-antiparticle pair, though, there's no reconstruction you can do that will show anything other than two particle tracks converging at a single point. Now, for reasons of mathematical convenience, you can choose to view this as a single particle reversing the direction of its motion through time, but there's no ambiguity about the existence of a single vertex, and the fact that both particles are observed at different locations in space at the same time. The dog and the cat will disagree about what constitutes a single instant of time at two different positions, but both will see a particle and its antiparticle existing in different places.
From the perspective of the alien, this isn't that exciting. Both the dog and the cat move from right to left at superluminal speeds, the cat somewhat slower than the dog. The big difference in terms of appearance would be that the alien would be utterly incapable of seeing anything behind it, because the light from events in the wake of its passage could never catch up.
I agree that there is a major difference between the underlying physical reality of the alien speeding by versus the particle/antiparticle pair that spontaneously appears and then annihilates.
I actually think that you're shortchanging the alien-eye-view of the situation. Let me focus on the dog...
If you draw light rays emanating from the time axis (the dog's worldline), you'll notice that for each moment in time, there is pair of light rays being sent out by the dog (or bouncing off of her). Actually, if you want to think about it in 3D space, you should think of it as a spherical shell of light emanating out from the dog at every instant.
When the alien is to the left of the dog's worldline, it will intercept the light rays that are moving out to the left and will see the dog getting older. However, when the alien crosses the dog's worldline something really interesting happens: it starts to catch up to the light rays that were going to the right. So after meeting the dog, the alien should start to see the dog aging in reverse---getting younger.
So the alien does indeed see some weird stuff!
Going with the thought experiment's idea that the metric is constant, there is a frame in which the alien travels at infinite speed from one side of the universe to the other. There isn't a Lorentz invariant property for the alien of moving from left to right or from right to left. In 3+1 dimensions the quotient group O(4)/SO(4) has four discrete components, with time-like forward/backward being invariant under the connected subgroup SO(4), but with no such invariant property for space-like 4-vectors.
But in a space-time in which the metric is locally Lorentzian, in GR it is usually /assumed/ that the manifold is both spatially orientable and temporally orientable (http://en.wikipedia.org/wiki/Orientability#Lorentzian_geometry: "a space-time is time-orientable if and only if any two observers can agree which of the two meetings preceded the other", Mark J. Hadley.The Orientability of Spacetime. Class Quantum Grav.19(2002)4565-4571 arXiv:gr-qc/0202031v4).
From the perspective of the alien, this isn’t that exciting.
Why not? Let's take the cat out of the scenario for the time being. The situation with just the dog and the alien should be symmetric: in the alien's frame of reference, the dog is moving superluminally. So the alien should see the dog appear and move in two different directions, just as the dog would see the alien appear and move in two different directions. In the alien's frame, the cat would just be a second superluminal object. The alien, if he were recording the scenario, could work out after the fact what happened, and deduce that the dog and cat are moving at different speeds. (What the cat's speed would be, I am not sure, because I'm not sure how to do a double Lorentz boost when one of the boosts is superluminal.)
Also, the alien should be able to see backwards. The speed of light in the alien's frame is the same as the speed of light in the dog's frame. The alien's backward direction may not be backward in the dog's frame, but it would be in his frame.
The only way the scenario with just the dog and the alien could not be symmetric is if there were something to tell us that the dog's frame is preferred. This is exactly what relativity says we can't have, as long as neither dog nor alien is accelerating.
Dumb Layperson Questions dep't:
I'm always skeptical of arguements that go "it can't be, therefore it isn't." In the present case, the well-known arguement that superluminal communication & travel are impossible "because" they would produce logical paradoxes with causality. Therefore:
1) Are there empirical data demonstrating that FTL travel/comms are never observed to occur and for which some alternative hypohesis is not tenable?
2) Are there solid maths that also demonstrate that FTL travel/comms are impossible? In which case how does this math interact with the stuff from kinetics wherein equations work regardless of whether the value for time is set as positive or negative?
3) What ever happened to tachyons, that are supposed to move backward across time?
4) What about the idea that any sort of causal paradox that might be produced, is instead isolated in a manner similar to that of a local universe: each element in the paradox becomes separated from the other so they both occur but cannot interact locally? (You can visualize this as each element of the paradoxical events getting trapped in vacuoles;-) (Or have I just come up with an inelegant way of describing the same situation you've already described but I failed to understand?)
In the superluminal dark, no cats are grey because the gamma rays from those receding are red-shifted into the blue , and the photons from those approching would torpedo any retina made by God or man
@comment #16: I imagine that different people will approach your questions differently. Here are some of my takes:
(1) We have *never* observed any signal or physical phenomenon that can travel faster than light. That doesn't mean that we won't ever do so, just that it's never happened. Furthermore, the aether hypothesis suggested that we should be able to observe light moving at different speeds and was soundly put to rest by the famous Michelson-Morley. experiments.
There are alternative hypotheses---Lorentz and Poincare derived the transformations at the heart of relativity by trying to save the aether theory. They proposed that physical bodies moving in the aether deform and their clocks run slow precisely so as to make it *look* like light has a universal speed. However, I would say that Einstein's more parsimonious approach is the more attractive one.
(2) Special relativity begins with the assumption that light moves at a speed that all inertial observers (observers who don't have any external forces applied to them) agree on. Remarkably, from that one can show that (a) if an object has a real mass (you know, the kind that we all have), then it is impossible for it to ever reach the speed of light. As you accelerate the object, more of the energy is effectively diverted into an increasing mass rather than an increasing speed. This means you need more force to maintain the same amount of acceleration. To get to the speed of light, you will need to expend an infinite amount of energy.
And yes, the maths here is quite solid!
(3) Tachyons in the context of special relativity are objects that move faster than light (incidentally, whether you take them to go backwards or forwards in time is a matter of perspective. The alien in Chad's example would be a tachyon). The problem with the naive view of tachyons is that they would require imaginary masses which is typically taken as a sign that they aren't physical.
On a more sophisticated level, there are situations that can fruitfully be described as tachyonic. The existence of a tachyon in your model typically means that your model is unstable or that you are approximating around an unstable equilibrium. The tachyon isn't really an object in this situation, it's more a sign that tells you that some sort of decay or change is going to occur that takes you to a different "sector" of your theory. I won't elaborate on this here.
(4) I'm not sure I follow here. There'd need to be a clear physical mechanism for this and I don't know of any plausible ones.
David @ 17:
Thanks! (And another question at the end of this.)
1) Agreed, parsimony wins over the aetheric equivalent of epicycles;-) If it was necessary to add a bunch of needless bits to save the idea of a variable speed of light, that doesn't work. (Though, I assume that the observation that photons slow slightly in water is accounted for without going back into the proverbial aether.)
2) Aha! You just supplied me with a big missing piece. (Here I should mention that I'm not a dumb-dumb but I'm dyslexic so I can get this stuff conceptually but I've never been able to get the maths.)
I've known that in the current body of theory, acceleration of objects toward c produces an increase in mass that theoretically becomes infinite (for which reason, when I speculate about interstellar migration, I assume the best we'll be able to do is a small single-digit percentage of c and I use .01c as an example). But I've always taken it "on faith" and never had an idea of the mechanism before (blush).
What you said was "more of the energy is effectively diverted into an increasing mass rather than an increasing speed." Keyword "diverted." Bingo!, that would seem to be the mechanism. Presumably Einstein's equations govern that diversion. That's the piece I was missing: the mechanism for the increasing mass approaching c.
Question: Would it be correct to consider that a form of "energy conversion," in a manner that's very roughly analogous to other types of energy conversion (e.g. sunlight reaches planet's surface and is converted to heat, or electrons in an LED are converted to light, etc.)? If not, then what?
3) Tachyons: from what you said, they appear to be a creation of theory in order to deal with mathematical errors or instabilities that shouldn't exist. Something like this: "if you get tachyons here, you made a mistake somewhere." Alternately, "a different sector of your theory," which suggests a different reference frame (yes I'd like to know what you meant by that but you said you weren't going into it further here, so I'll park that question for the moment and look for some other opportunity to ask someone;-)
4) Apologies for not marking that item off with "the following isn't science, it's a wild speculation." What I was looking for were ways the "paradox" might be "solved." Something like Everett's many-worlds theory: "the universe splits here" so each branch of the paradox exists in a separate universe.
For example (using the nonviolent version of the Grandfather Paradox), you call your grandfather on the tele-time-phone and ask him to use condoms for a month. You don't ever find out if he actually does so. But if he does, then something similar to your local universe splits, whereby your existence continues in the universe where he does not use condoms (or a condom fails), and another timeline occurs into a different universe where the condoms work and you don't exist: but you never get to observe the second universe.
To my mind that's approximately as counterintuitive as the idea that the universe splits at every wavefunction collapse.
And while we're on that subject, another question that's been bugging me for years:
Where does Everett get the energy needed to create multiple universes at every wavefunction collapse?, or, are the splits in his theory confined to the immediate locality of each particle? (I'm highly skeptical of "the whole universe splits" but I'm agnostic about "the immediate locality of the particle splits," and in any case I don't see where the energy would come from to duplicate a universe either generally or locally.)
Hi G,
1) Light does propagate more slowly in a medium other than vacuum. This is essentially due to the fact that light---thought of as an electromagnetic wave---interacts with the atoms or molecules making up the material. This interaction is often characterized as the photons of the light being absorbed and re-emitted by the electrons in the medium, but that isn't quite right. The actual story is more complicated. But the gist of it is as I said, an interaction between the light and the medium.
(and no aether is needed! We have a real medium in this case.)
2) I'm glad that this explanation helps. Let me try to be a bit more precise instead of speaking about "effective" increases in mass. Einstein derived a formula for the total energy of a freely moving object. This formula combines the rest energy and the kinetic energy of the object as the two contributions. However, the kinetic energy is different in form from the non-relativistic one that we learn in school. In particular, it is strongly modified at very high speeds so that it goes to infinity as the speed approaches that of light.
The kinetic energy and rest energy (the energy inherent in the mass you'd measure when the object is at rest) combine in a rather natural way to give you the following for the total energy:
m c^2 / sqrt(1-v^2/c^2)
where m is the mass as measured at rest. Some people take this total energy and divide by c^2 to get a quantity that is called "relativistic mass". You can think of this as a generalization of the rest mass which includes the effects of it being in motion. If you look at the formula above you'll notice that the total energy, and thus, the relativistic mass increases to infinity as the speed v approaches the speed of light c.
Some people prefer not to describe things in terms of relativistic mass since this type of mass is completely equivalent to the total energy of the object. Instead, you can say that since energy and mass are interconvertible, energy itself also resists being accelerated. So if the energy stored by an object (say its kinetic energy) goes up, then it becomes harder to accelerate, so you have to push it harder.
So the answer to your follow up question is that this is not exactly the same thing as transferring energy from one store of energy to another, such as solar to chemical. Rather, the kinetic energy has an in-built resistance to acceleration that is basically the same as the resistance that the Newtonian concept of mass captures. As the kinetic energy goes up, the overall inertia of the object goes up.
That said, the energy stored up in the rest mass of an object can indeed be unlocked. In fact, turning this story around, we find that the majority of the mass in our bodies is actually in the form of the binding energy! The nuclei of the atoms in our bodies are made of protons and neutrons. These protons and neutrons are themselves bound states of subatomic particles called quarks and gluons. The quarks themselves have tiny masses, but it is the *energy* that binds them together that is responsible for most of the mass in a proton or a neutron.
3) I'd put this a bit differently. There is nothing in special relativity that mathematically forbids one from asking what the properties of an object would be if it travels faster than light. However, when you do this, you discover the bizzaro result that the mass would have to be described by an imaginary number. So at first blush you might say, well the theory is saying GIGO---garbage in, garbage out. The assumption that this thing can be going faster than light is garbage, so I'm getting garbage results.
However, it turns out that there is a utility to the notion of imaginary mass or energy. This will likely be cryptic and will probably set off more questions than answers since I don't have time to get into all the details, but here goes!
Consider the following mathematical functions:
e^(-gt)
e^(i E t)
where g and E are some constants chosen in units of inverse time (let's say in Hertz). The first function is just an exponentially decaying function. As time gets big, the function approaches zero exponentially fast.
The second function is an oscillatory function. Yes, it is imaginary, but you can take its real part and you get a cosine that oscillates with a frequency determined by the constant E.
In quantum theory, a free particle is described by a wavefunction that looks like this sort of persistent oscillatory function. The constant E really is related to the free particle's energy in this case.
A particle that decays isn't actually free, but its wavefunction will look like a damped oscillatory function, that is, it will look like a product of the two functions above. The constant E will again be related to the energy, and the constant g will set the time scale over which this particle decays. So you end up with a wavefunction that is sort of like this:
e^{i E t} e^{-gt}
but this can be rewritten as
e^{iEt - gt}
Now let me introduce a new notation. Let the complex number
q = E + ig
be the "complexified energy" of this particle. Notice that the real part is just the ordinary energy, while the imaginary part is related to the decay constant. We can rewrite the "wavefunction" as
e^{i q t}
this is the same information as before, but its a nice notation. Intriguingly, you can see that giving the energy an imaginary part yields a description of something unstable---something that decays away. This is a hint that tachyons are somehow connected to instabilities.
The analogy can be pushed further. Again, you won't find that tachyons can be observed as real, physical particles. Rather, they represent fields that are unstable.
I'll end with what may be an enigmatic note: the version of string theory that is used to introduce the subject---the so-called bosonic string theory---has a tachyon as its lowest energy field. This is taken to imply that bosonic string theory is unstable and requires completion by embedding into some other type of theory where the theory may evolve into a stable regime (getting rid of the tachyon). This is still an area of active research in string theory.
4) Ah, I think I see---the idea here is that paradox is avoided by thinking of the universe as branching off so that if you go back in time and do something, your time line ends up going to a different branch, not intersecting itself in a potentially contradictory manner.
That's certainly a valid way of trying to solve time-travel paradoxes, but there aren't really physical mechanisms that suggest that such a thing actually can happen. I suppose that if you are a many worldser (someone who subscribes to the many worlds interpretation of quantum theory) then you might concoct some explanation of this as interference between different branches of the universal wavefunction...but color-me-skeptical! (I'm actually rather skeptical of the whole many worlds approach in general. It's actually a much less straightforward interpretation than meets the eye. Much of its messiness is ignored or obfuscated in popular discussions).
I've got to run, but I'll try to answer your last question when I have some time.
Alright G, let's see if we can tackle that last question.
You asked about where all that energy comes from in Everett's many worlds interpretation for the creation of new universes or at least the "unzipping" of a universe at certain events in time.
Well, first one needs a more precise model of what many worlds is and what these universes are. The simplest approach is to start with the assumption that the state of the entire universe is described by a wavefunction that I'll call Psi. Let me point out from the get-go that this is actually a major assumption---something that often is glossed over in discussions about many worlds. It is not at all clear that our universe and its evolution can indeed be described by the assumption that its dynamical state is captured by a wavefunction evolving via the Schrodinger equation. What if the universe is fundamentally an "open" quantum system? In that case, the dynamics can be much harder to grasp...
But, taking the plunge, assume that Psi describes the universe and that there is a quantum law (a Hamiltonian) that gives us the evolution of Psi via the Schrodinger equation. According to many worlds, that's all there is.
So, where are the many branches of the universe (or multiverse)? They come from how you can decompose Psi into different terms. This is similar to how you can decompose a position vector into x, y, or z components. The idea is that at any given time, there is a decomposition of Psi into (probably infinitely) many components. If all goes well with the interpretation, our universe is described by one such component or branch, while other universes correspond to the different branches. As time evolves, macroscopic interactions with microscopic objects leads to decoherence, a process whereby initially "quantum" looking things tend toward looking more classical. It's thought that this describes how universes split into new branches.
So what about energy? Well, the simplest answer to write down is that the universe may not have a well-defined total energy. The components of Psi that describe the different universe-branches also don't have to have a well-defined energy. So there's no sense in which "splitting" would have a well defined energy either.
But suppose that it just so happened that the branches that describe macroscopically familiar universes do have precise energies associated with them (technically we'd say that these branches are "eigenstates" of the universe's Hamiltonian---it's energy operator). If that's the case, then each branch has a total energy of its own that won't change as it evolves, so within a universe-branch, there will be conservation of the total energy.
Actually, I'm not sure how to make the second picture consistent with the idea of branching. It seems to me that in such a scenario (where the energies are well defined for each branch) then the universal wavefunction would have to come with a predefined branching structure that is already in place. That's rather unlikely.
So the first answer is probably a better one: total energy is probably not a well defined property of the various branches that make up the universal wavefunction. That precludes any problems with the "creation" of new energy when a split occurs.
As a parting note, I'll point out that the total energy of the universe is actually not a generally well defined concept in general relativity either. For example, our universe probably does not have a well-defined total energy. This occurs because space itself is able to evolve in non-trivial ways in general relativity, and the dynamics of space ends up potentially messing up any general definition of total energy you might try to dream up.