Entangled in the Past: "Entanglement Between Photons that have Never Coexisted"

In which we do a little ResearchBlogging to look at a new paper about weird quantum effects, entangling two photons that never both exist at the same time.

------------

I'm teaching full-time this term, but I've blocked out Thursdays as a day when I don't do class- or chair-related work. Usually, this means trying to write something on the work-in-progress, but I finished a short thing in the morning that needed to sit for a few hours before I looked at it again, which left a nice opportunity for some blogging. And, conveniently, somebody retweeted a New Scientist story about an arXiv preprint that is right in the ResearchBlogging wheelhouse, as it were. I'm not sure where it's been sent, so it's not technically peer-reviewed yet, save in the minimal pass-the-laugh-test sense that it takes to get on the arXiv, but it's a real article that I'll explain in imaginary Q&A format.

So, this is yet another entanglement paper? Yep. It's a real growth area in the literature these days. This is another paper pushing the boundaries of the weird phenomena of quantum entanglement.

In this case, as the paper says, they're creating entanglement between two photons that never exist at the same time. One of them has already been detected (and thus ceased to exist) by the time the other is created. And yet, measurements of the states of the two show exactly the correlations you expect for an entangled system.

You're not going to make a bunch of dumb Halloween-themed jokes about ghosts and zombies, are you? Because that would suck. No, I'll leave the ghosts and zombies out of it. I warn you, though, that the New Scientist piece isn't so considerate.

Thank you. So, anyway, how do you go about entangling a photon with something that doesn't exist any more? The basic method is nothing all that new-- it's just "entanglement swapping," which we've talked about before, also in a context involving weird time effects. This is just a different twist on the same sort of idea: two entangled pairs of photons are created, and then a joint measurement of one photon from each pair creates an entanglement between the other two. The twist this time is that one of the photons from the first pair has already been measured before the second pair is even created.

How do they manage that, anyway? It's pretty clever, but a little confusing to follow in the paper itself, so I'll modify their figures a little to make it clearer. The basic apparatus is sown in the featured image at the top of this post, and consists of a special crystal (marked "BBO" in the center) that takes light from a UV laser and produces two infrared photons in an entangled state.

In the first step of the experiment, photon 1 and photon 2 are created, represented by the red circles in this figure:

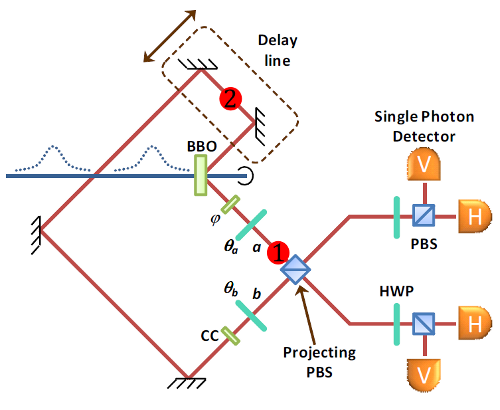
Step one of the experiment: photons 1 and 2 are created. Photon 1 goes straight to the detector, photon 2 goes off into a delay line.

Photon 1 goes directly to the collection of beamsplitters and detectors in the lower right part of the diagram, which measure its polarization state. Photon 2 goes off to the delay line in the upper left.

What's a delay line? It's just a path followed by a light beam that delays it for some time. In this case, it just bounces off a bunch of widely spaced mirrors, traveling a path that's some 31 meters longer than the distance from the crystal to the state detector. That path also wraps around the apparatus, so at the end of it, photon 2 enters the state detector from the other side.

So you measure its state long after you measured the state of photon 1? Not exactly. You see, the length of that path is carefully chosen so that by the time photon 2 comes back around to the detector, a second UV laser pulse has arrived at the crystal, creating a new pair of entangled photons, photons 3 and 4, represented by the blue circles:

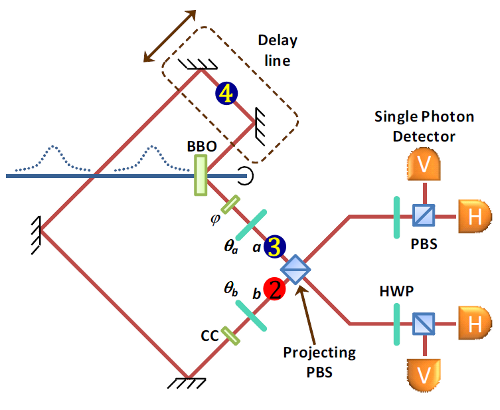
Step two of the experiment. Photon 2 comes back to the detector at the same time as the newly-created photon 3, and a joint measurement of the two together entangles photon 1 with photon 4.

So, wait, photon 2 and photon 3 hit the detector at the same time? How do you tell them apart? That's the clever bit: you can't. There's no way to know which photon is which; all you can say is whether the two have the same polarization or opposite polarizations. That joint measurement of the two photons is exactly what you need to swap the entanglement of the two pairs. After you make the joint measurement of photon 2 and photon 3, photon 1 and photon 4 are in an entangled state.

OK, but you already measured photon 1. And what happened to photon 4, anyway? Photon 4 follows the same path that photon 2 did, arriving at the detector by itself, a hundred-odd nanoseconds later:

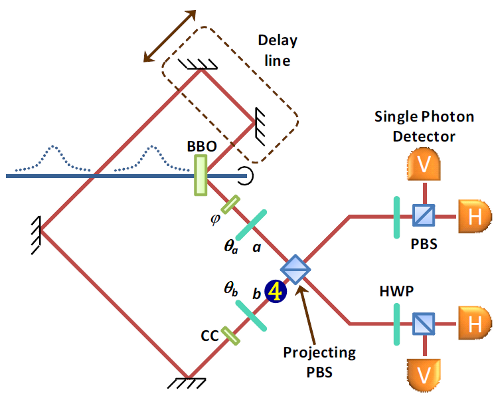
Step 3 of the experiment: photon 4 passes through the delay line and comes to the detector, which measures its polarization.

This acts to measure its polarization state, just as happened with photon 1.

So, how do you know it's entangled? Well, after the measurement is over, you compare the measurements of photon 1 and photon 4, and the results of the joint measurement of photons 2 and 3, and see that they are correlated with each other in the way that you expect. They do this for a whole bunch of different settings of their detector, in a way that allows them to map out the full quantum state, and what you see is exactly what you expect for an entangled state.

Even though photon 1 was destroyed before photon 4 was created? Exactly.

Is this one of those screwy relativity type experiments where some fast-moving observer would see the measurements happening in a different order, so there's some frame where all four photons exist at the same time? No. The particles involved move at the speed of light, and there's no way to change that speed. Also, all three state measurements take place at the same detector. There's no way to move that will change the order of events enough to have all four existing simultaneously.

And is there some weird cosmic conspiracy loophole to this experiment? Maybe. They don't go into it, but I suspect the fact that all four photons come from the same crystal and are detected by the same detector allows some interpretation of the results in which non-locality doesn't need to be invoked-- some kind of "memory" effect in the detector that makes photon 4's measurement results match up with photon 1's.

Even so, though, this would be a different sort of weird confounding effect than the weird confounding effects needed to explain other experiments where the constraints on locality are much stronger. And while you could construct a theory where everything is always local, but all these different effects come up in different experiments, at some point you're just accumulating epicycles. It's kind of ugly and inelegant, and entanglement is a better alternative.

OK, but doesn't the fact that you measured photon 1 mean that photon 2 is in a definite state when it hits the detector, not the indeterminate state you usually have in entanglement experiments? I haven't worked it all out in detail, so it might be possible to think of this as just a definite state being projected from photon 2 to photon 4. But then you're still doing something a little weird-- it's then a quantum teleportation kind of thing, teleporting a state into the future via a chain of entanglement. Which is also kind of cool.

I guess. But is there any point to this? Yes, if you think in terms of quantum information processing. One thing people might like to do is to exchange information between widely separated sites, using a kind of quantum analogue of the Internet. If you want to do that, effectively entangling the state of a particle in a lab in Jerusalem where this experiment was done with the state of a different particle, say in Anton Zeilinger's lab in Vienna, you might worry that you need to somehow store the particles in Jerusalem long enough for their entangled partners to arrive in Vienna. That's kind of a tricky business, and gets harder the longer the distance traveled.

What this suggests is that you don't have to go to those lengths. You can send the entangled partners off from Jerusalem, then immediately go through whatever operations you need to do there, and whenever the partner particles show up in Vienna, Herr Doktor Professor Zeilinger can do whatever he needs to do there, and the entanglement that's produced will make sure that the results of measurements in Jerusalem are coordinated with those in Vienna in exactly the way quantum mechanics predicts.

So, this is another step on the road to getting quantum spam from evil squirrels in Nigeria? I'm not sure they have evil squirrels in Nigeria-- though the furry little bastards do seem to get around-- but yes, in a manner of speaking. I doubt quantum computers will ever be used for sending email, though, but that's probably a subject for another time.

A time which will be inextricably bound up with this one? Entangled, in a manner of speaking? If you really want to end this on a strained joke, yes. We're done now.

E. Megidish, A. Halevy, T. Shacham, T. Dvir, L. Dovrat, & H. S. Eisenberg (2012). Entanglement Between Photons that have Never Coexisted arXiv arXiv: 1209.4191v1