Driving a Simulated Pendulum

Some time back, I spent a bunch of time writing a VPython program that simulated the motion of a pendulum, which turned out to do some strange things. In the comments to that, there were two things worth mentioning: first and foremost, Arnoques at #5 spotted a small error in the code that fixes the odd behavior noted in that post-- when I corrected it, the stretch needed to keep the pendulum swinging smoothly without oscillating in and out along the string was exactly what you would expect (the "factor" plotted in that earlier post is infinitesimally smaller than 1.0-- I got bored trying to find out exactly where). Of course, I didn't get to test that until after comments were closed-- maybe I'll edit the post to add a note.

The other interesting comment was #4, from Blaise Pascal (no relation), who made a request for further simulation:

What would happen if you simulated a driven pendulum? Start with the pendulum at rest (the easiest condition to calculate the necessary stretch at), and then simulate a periodic “nudge” on the pendulum to get it swinging (and to increase it’s swing).

One way to nudge it would be to change the x coordinate of the top of the string from +epsilon to -epsilon when the pendulum is moving right to left, and from -epsilon to +epsilon when the pendulum is moving left to right, as long as the swing wasn’t too great, and epsilon was inversely related to the spring constant.

Being a great big nerd, I couldn't resist this, and so the next time I felt like puttering with computer code, I added a periodic drive to the system. I didn't quite do the exact thing suggested in the comment-- rather, I put in an arbitrary period for switching the pivot point between plus and minus 1cm left and right of the origin. I probably could've stuck in a sinusoidal drive, but instead I just used if-then statements: when the time hit a half-integer multiple of the period, the pivot instantaneously jumps left, then jumps back to the right at integer multiples.

(Foolishly, I thought this would be simpler. For my folly, I ended up spending a bunch of time discovering odd features of modulo arithmetic in VPython...)

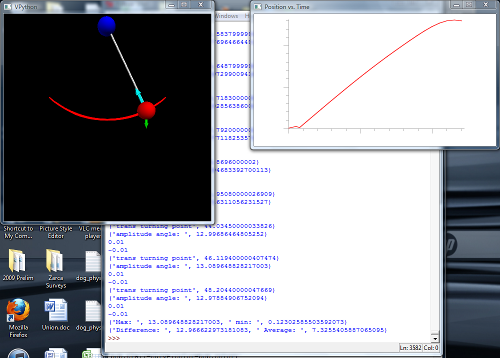
This does, in fact, do more or less what you would hope. I started it with a small amplitude (three degrees, because three is the magic number), and for most choices of driving period, it doesn't change much. Get close to the natural resonance of the pendulum, though (a period of about 2.03s for the parameters I was using), and the amplitude would get big. You can see the output up at the top of the post in the "featured image," or look at it right here:

A simulated pendulum driven near resonance.

The window with a black background shows the cartoon pendulum, and the graph is the angle the string makes at the rightmost point of the swing, plotted for each oscillation. As you can see, there's a little hiccup at the start, then this grows steadily, as the drive dumps energy into the system.

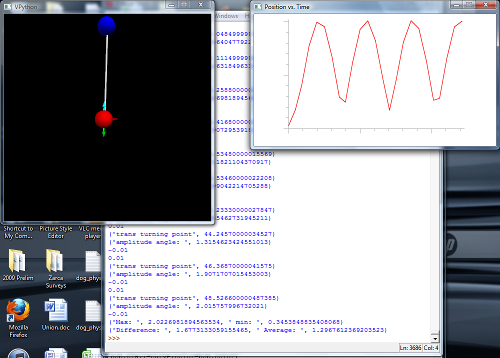
Having made this work, of course, I needed something quantitative to do with this. And though the actual code is way more complicated than I'll spend time on in our real intro classes, I wanted to keep this to terms that I could easily explain to students in intro mechanics, so my first thought was to just let it run for a while and use the final turning point as a measure of how much the drive affected things. This runs into a problem, though, because when you go a little off-resonance, you get something that looks like this:

The simulated pendulum, driven slightly off resonance.

You can see that there are oscillations of the maximum amplitude point. That does some odd things if you look at the behavior just through the last turning point, or even the maximum amplitude during the running of the program (50 simulated seconds). The frequency response seems to pick up some "wiggles" (technical term) as the exact point where you catch the oscillation moves around. So instead, trying to keep this in intro-mechanics terms, I used an average of the turning point positions for the entire oscillation.

(You can see, by the way, that the nearly-resonant case also shows some hint of this oscillatory behavior, just with a really long period. I think there are two reasons for this: 1) I'm not exactly at the resonance there, and 2) The oscillation is slightly anharmonic-- as the amplitude gets big, it takes longer to complete a swing, and eventually the oscillation period gets significantly longer than the drive period.)

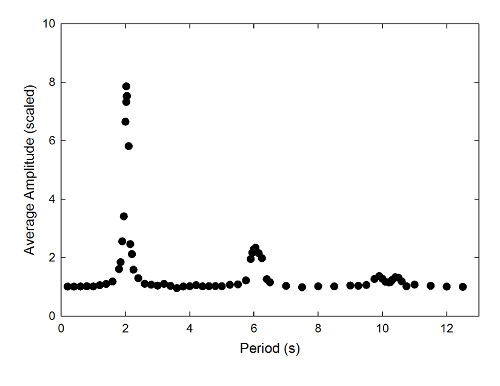
Having done all this, what's the result? Well, here's the pay-off, a graph of response versus oscillation period:

The response of a simulated pendulum to driving at different periods.

The vertical axis here measures the average turning point angle divided by the initial angle, so this is a dimensionless arbitrary units kind of deal. You can see a large and narrow peak at a drive period of just over 2 seconds (around 2.04, and it took forever to get the data for this), exactly as you expect. This is the point where the drive is exactly in synch with the swing-- if you imagine the pendulum as a kid on a swing, this corresponds to giving her a push left when she hits the rightmost point, and a push to the right when she hits the leftmost point.

The other thing that took forever to figure out is that there are two other peaks here: one at a drive period of a bit over 6 seconds, and another at a bit over 10 seconds. It took a long, long time to figure out what was going on with these, and for quite a while I thought I had a bug in the program. But I realized last night what the deal is.

That 6s drive period is very nearly three times the natural period, and that's what threw me-- I didn't understand why I would get a peak at three times, but not two or four. That's because I was thinking of this like a playground swing, with a push on only one side of the pendulum-- in that case, a drive period of two times the natural period would work just fine. All that means is skipping every other swing.

But, of course, that's not what's going on here-- this system is pushed on both ends. So, a period of twice the natural period gets a push to the left when it hits the rightmost point, then when it returns to the rightmost point on the next oscillation (halfway through the drive period) it gets a push to the right, which undoes the good done by the first push.

At three times the period, though, everything works nicely again. You get a push to the left at the rightmost point, then nothing for one and a half of the natural oscillations. That means you skip the next return to the rightmost point, but deliver the next, rightward push, half an oscillation later-- that is, at the leftmost point. So, you're synched up with the swing on both ends, and the oscillation gets big.

This also explains the peak at 10s drive period-- that's five times the natural period, and thus amounts to skipping two-and-a-half oscillations. The amplitude of the higher period peaks is smaller in large part because they don't get in as many pushes-- this was running for a fixed 50s every time, so the natural period drive got 24 pushes in, the three-times drive eight, and the five-times drive only about 4. If I changed it to run for a set number of pushes, rather than a fixed time, those amplitudes might be bigger, but I didn't realize that until I had already spent hours messing with this, and I wasn't about to start over yet again. Consider it homework, if you like, and send it to Rhett to be graded.

This is not without some minor mysteries, of course-- in particular, I don't know why that 10s period peak is a doublet. This might be an artifact of the short drive time, or something else. It's very repeatable, though, and there might be something going on with the 6s peak as well, which is clearly broader than the 2s one. But, all in all, this worked out pretty nicely, and I learned something cool along the way. So, while this is almost certainly never going to get used in a class, it was worth the fooling around.

Future directions, should I feel like noodling around some more: 1) Looking at driving oscillations along the string (which are at a different frequency, and not tracked in the current iteration of the program), and 2) Adding damping to the system, which should reduce the height and increase the width of these resonant peaks. I could also play with the phase a little-- there's a little hiccup at the start of the amplitude graph every time that I realized belatedly is because I have the initial phase wrong (again, I realized this last night, but wasn't about to start over). Moving the push to different points in the oscillation might be interesting, though I suspect it would introduce me to a whole new set of stupid modulo division bugs that might drive me insane.

And that's what's up in the world of simulating simple physical systems.