I followed up my ranty-y post about "Sports Science" with an experimental investigation over at Forbes, tossing a football around on the deck out back and then doing video analysis of the bounces. This provided a wealth of data, much of it not really appropriate for over there, but good for a physics post or two here.
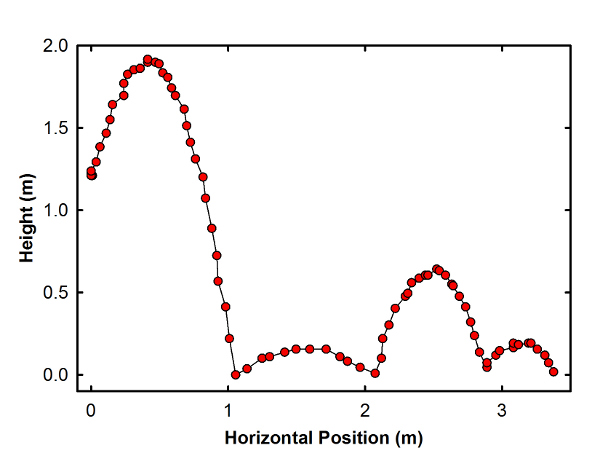
One of the trajectories I looked at was this "forward bounce":
Here's the trajectory reconstructed in Tracker:
This is notable because not only does it bounce forward, it includes one of those big pop-up bounces that take people off guard. I talked about this over at Forbes, too, but it's nice to have a clear example.
In that post, I asserted that the big bounce is a result of converting some rotational kinetic energy of the tumbling ball to center-of-mass kinetic energy. Which, of course, made me wonder whether you can clearly measure that in the video. You can, as it turns out, which is why I'm writing this post.
What I did to make the above trajectory was to go through the video in Tracker and mark the center of the ball (the garish green laces on the black ball are well suited to this). To look at rotation, I put the same clip into Tracker, but instead of marking the center of mass, I made two trajectories, one for each end of the ball. That let me do a "relative position" of one end compared to the other, just by taking the difference between the measured positions. Actually, I get both a relative x and relative y coordinate, but this only needs one of the two; I used the vertical, because it's a little cleaner:
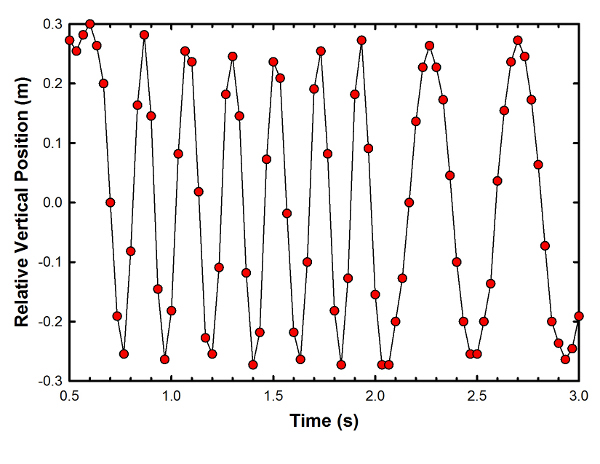 The difference between vertical coordinates for the two ends of the football, as a function of time.
The difference between vertical coordinates for the two ends of the football, as a function of time.
This goes from positive to negative as the ball rotates, and you can clearly see the change in the tumbling at a time of just under 2s, when the big bounce occurs. The rotation period goes from roughly 0.21s to roughly 0.43s, corresponding to a rather substantial reduction in the rotational energy. About three-quarters of the energy that was in the spin of the ball gets turned into center-of-mass kinetic energy (and lost to thermal energy), which is why you get a big increase in the bounce height.
You could probably do some more quantitative analysis of this, either using the mass and known shape of the football to estimate its moment of inertia and check the energy change, or using the change in the maximum height to estimate the change in potential energy and then work backwards to an estimate of the moment of inertia. These are both complicated by the energy loss on the bounce, and I'm home with a sick Pip today, so I'm not going to bother. Consider those extra-credit homework, if you like, and send your answers to Rhett Allain for grading.
------
The science blog reader survey I've been plugging at the end of my physics posts is coming to an end soon-- this Friday, in fact. It's part of Paige Jarreau's postdoctoral research on online communications, so please take a few minutes and respond-- it's for SCIENCE!

Nice example. This doesn't happen with a basketball because of its symmetry.
This relates to spectroscopy...what frequencies are absorbed by certain molecules relates to whether they are symmetrical or not and what vibrational and rotational modes they have.